Question Number 74882 by ajfour last updated on 03/Dec/19

Commented by ajfour last updated on 03/Dec/19

$${If}\:{each}\:{small}\:{blue}\:{triangles} \\ $$$${have}\:{the}\:{same}\:{area},\:{and}\:{each} \\ $$$${small}\:{quadrilaterals}\:{have}\:{the} \\ $$$${same}\:{area},\:{find}\:{ratio}\:{of}\:{length} \\ $$$${to}\:{breadth}\:{of}\:{the}\:{outer}\:{rectangle}. \\ $$
Commented by mind is power last updated on 03/Dec/19
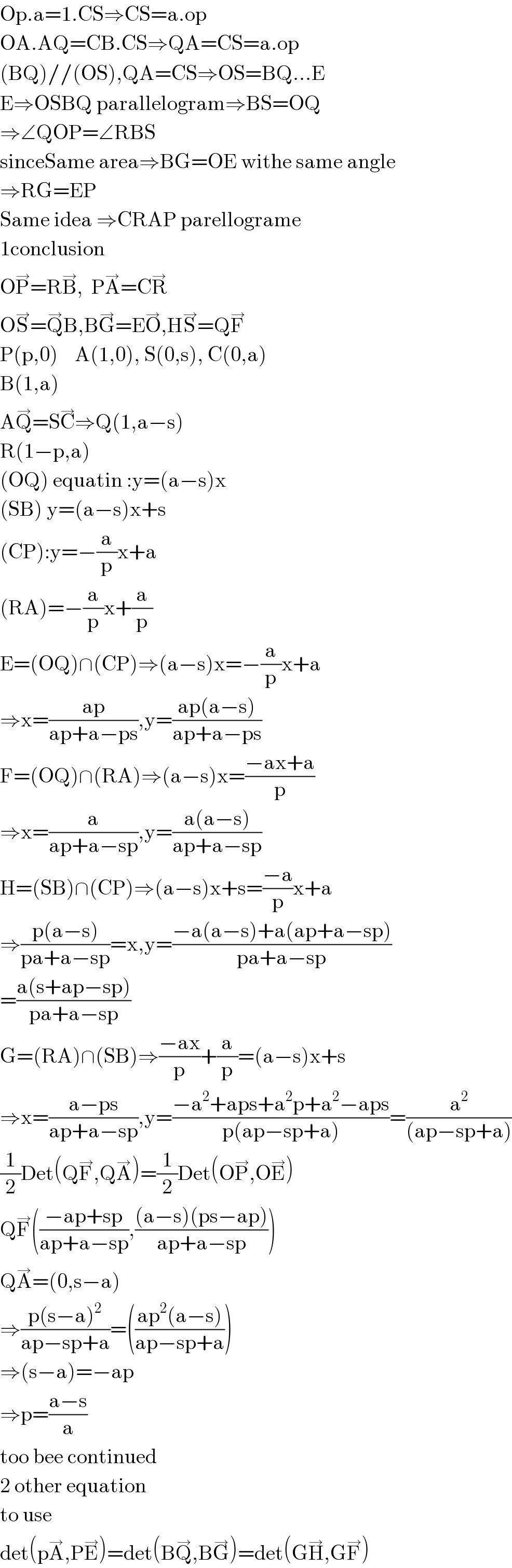
$$\mathrm{Op}.\mathrm{a}=\mathrm{1}.\mathrm{CS}\Rightarrow\mathrm{CS}=\mathrm{a}.\mathrm{op} \\ $$$$\mathrm{OA}.\mathrm{AQ}=\mathrm{CB}.\mathrm{CS}\Rightarrow\mathrm{QA}=\mathrm{CS}=\mathrm{a}.\mathrm{op} \\ $$$$\left(\mathrm{BQ}\right)//\left(\mathrm{OS}\right),\mathrm{QA}=\mathrm{CS}\Rightarrow\mathrm{OS}=\mathrm{BQ}…\mathrm{E} \\ $$$$\mathrm{E}\Rightarrow\mathrm{OSBQ}\:\mathrm{parallelogram}\Rightarrow\mathrm{BS}=\mathrm{OQ} \\ $$$$\Rightarrow\angle\mathrm{QOP}=\angle\mathrm{RBS} \\ $$$$\mathrm{sinceSame}\:\mathrm{area}\Rightarrow\mathrm{BG}=\mathrm{OE}\:\mathrm{withe}\:\mathrm{same}\:\mathrm{angle} \\ $$$$\Rightarrow\mathrm{RG}=\mathrm{EP} \\ $$$$\mathrm{Same}\:\mathrm{idea}\:\Rightarrow\mathrm{CRAP}\:\mathrm{parellograme} \\ $$$$\mathrm{1conclusion} \\ $$$$\mathrm{O}\overset{\rightarrow} {\mathrm{P}}=\mathrm{R}\overset{\rightarrow} {\mathrm{B}},\:\:\mathrm{P}\overset{\rightarrow} {\mathrm{A}}=\mathrm{C}\overset{\rightarrow} {\mathrm{R}} \\ $$$$\mathrm{O}\overset{\rightarrow} {\mathrm{S}}=\overset{\rightarrow} {\mathrm{Q}B},\mathrm{B}\overset{\rightarrow} {\mathrm{G}}=\mathrm{E}\overset{\rightarrow} {\mathrm{O}},\mathrm{H}\overset{\rightarrow} {\mathrm{S}}=\mathrm{Q}\overset{\rightarrow} {\mathrm{F}} \\ $$$$\mathrm{P}\left(\mathrm{p},\mathrm{0}\right)\:\:\:\:\mathrm{A}\left(\mathrm{1},\mathrm{0}\right),\:\mathrm{S}\left(\mathrm{0},\mathrm{s}\right),\:\mathrm{C}\left(\mathrm{0},\mathrm{a}\right) \\ $$$$\mathrm{B}\left(\mathrm{1},\mathrm{a}\right) \\ $$$$\mathrm{A}\overset{\rightarrow} {\mathrm{Q}}=\mathrm{S}\overset{\rightarrow} {\mathrm{C}}\Rightarrow\mathrm{Q}\left(\mathrm{1},\mathrm{a}−\mathrm{s}\right) \\ $$$$\mathrm{R}\left(\mathrm{1}−\mathrm{p},\mathrm{a}\right) \\ $$$$\left(\mathrm{OQ}\right)\:\mathrm{equatin}\::\mathrm{y}=\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x} \\ $$$$\left(\mathrm{SB}\right)\:\mathrm{y}=\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x}+\mathrm{s} \\ $$$$\left(\mathrm{CP}\right):\mathrm{y}=−\frac{\mathrm{a}}{\mathrm{p}}\mathrm{x}+\mathrm{a} \\ $$$$\left(\mathrm{RA}\right)=−\frac{\mathrm{a}}{\mathrm{p}}\mathrm{x}+\frac{\mathrm{a}}{\mathrm{p}} \\ $$$$\mathrm{E}=\left(\mathrm{OQ}\right)\cap\left(\mathrm{CP}\right)\Rightarrow\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x}=−\frac{\mathrm{a}}{\mathrm{p}}\mathrm{x}+\mathrm{a} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{ap}}{\mathrm{ap}+\mathrm{a}−\mathrm{ps}},\mathrm{y}=\frac{\mathrm{ap}\left(\mathrm{a}−\mathrm{s}\right)}{\mathrm{ap}+\mathrm{a}−\mathrm{ps}} \\ $$$$\mathrm{F}=\left(\mathrm{OQ}\right)\cap\left(\mathrm{RA}\right)\Rightarrow\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x}=\frac{−\mathrm{ax}+\mathrm{a}}{\mathrm{p}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{a}}{\mathrm{ap}+\mathrm{a}−\mathrm{sp}},\mathrm{y}=\frac{\mathrm{a}\left(\mathrm{a}−\mathrm{s}\right)}{\mathrm{ap}+\mathrm{a}−\mathrm{sp}} \\ $$$$\mathrm{H}=\left(\mathrm{SB}\right)\cap\left(\mathrm{CP}\right)\Rightarrow\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x}+\mathrm{s}=\frac{−\mathrm{a}}{\mathrm{p}}\mathrm{x}+\mathrm{a} \\ $$$$\Rightarrow\frac{\mathrm{p}\left(\mathrm{a}−\mathrm{s}\right)}{\mathrm{pa}+\mathrm{a}−\mathrm{sp}}=\mathrm{x},\mathrm{y}=\frac{−\mathrm{a}\left(\mathrm{a}−\mathrm{s}\right)+\mathrm{a}\left(\mathrm{ap}+\mathrm{a}−\mathrm{sp}\right)}{\mathrm{pa}+\mathrm{a}−\mathrm{sp}} \\ $$$$=\frac{\mathrm{a}\left(\mathrm{s}+\mathrm{ap}−\mathrm{sp}\right)}{\mathrm{pa}+\mathrm{a}−\mathrm{sp}} \\ $$$$\mathrm{G}=\left(\mathrm{RA}\right)\cap\left(\mathrm{SB}\right)\Rightarrow\frac{−\mathrm{ax}}{\mathrm{p}}+\frac{\mathrm{a}}{\mathrm{p}}=\left(\mathrm{a}−\mathrm{s}\right)\mathrm{x}+\mathrm{s} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{a}−\mathrm{ps}}{\mathrm{ap}+\mathrm{a}−\mathrm{sp}},\mathrm{y}=\frac{−\mathrm{a}^{\mathrm{2}} +\mathrm{aps}+\mathrm{a}^{\mathrm{2}} \mathrm{p}+\mathrm{a}^{\mathrm{2}} −\mathrm{aps}}{\mathrm{p}\left(\mathrm{ap}−\mathrm{sp}+\mathrm{a}\right)}=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{ap}−\mathrm{sp}+\mathrm{a}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Det}\left(\mathrm{Q}\overset{\rightarrow} {\mathrm{F}},\mathrm{Q}\overset{\rightarrow} {\mathrm{A}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Det}\left(\mathrm{O}\overset{\rightarrow} {\mathrm{P}},\mathrm{O}\overset{\rightarrow} {\mathrm{E}}\right) \\ $$$$\mathrm{Q}\overset{\rightarrow} {\mathrm{F}}\left(\frac{−\mathrm{ap}+\mathrm{sp}}{\mathrm{ap}+\mathrm{a}−\mathrm{sp}},\frac{\left(\mathrm{a}−\mathrm{s}\right)\left(\mathrm{ps}−\mathrm{ap}\right)}{\mathrm{ap}+\mathrm{a}−\mathrm{sp}}\right) \\ $$$$\mathrm{Q}\overset{\rightarrow} {\mathrm{A}}=\left(\mathrm{0},\mathrm{s}−\mathrm{a}\right) \\ $$$$\Rightarrow\frac{\mathrm{p}\left(\mathrm{s}−\mathrm{a}\right)^{\mathrm{2}} }{\mathrm{ap}−\mathrm{sp}+\mathrm{a}}=\left(\frac{\mathrm{ap}^{\mathrm{2}} \left(\mathrm{a}−\mathrm{s}\right)}{\mathrm{ap}−\mathrm{sp}+\mathrm{a}}\right) \\ $$$$\Rightarrow\left(\mathrm{s}−\mathrm{a}\right)=−\mathrm{ap} \\ $$$$\Rightarrow\mathrm{p}=\frac{\mathrm{a}−\mathrm{s}}{\mathrm{a}} \\ $$$$\mathrm{too}\:\mathrm{bee}\:\mathrm{continued} \\ $$$$\mathrm{2}\:\mathrm{other}\:\mathrm{equation} \\ $$$$\mathrm{to}\:\mathrm{use} \\ $$$$\mathrm{det}\left(\mathrm{p}\overset{\rightarrow} {\mathrm{A}},\mathrm{P}\overset{\rightarrow} {\mathrm{E}}\right)=\mathrm{det}\left(\mathrm{B}\overset{\rightarrow} {\mathrm{Q}},\mathrm{B}\overset{\rightarrow} {\mathrm{G}}\right)=\mathrm{det}\left(\mathrm{G}\overset{\rightarrow} {\mathrm{H}},\mathrm{G}\overset{\rightarrow} {\mathrm{F}}\right) \\ $$
Commented by ajfour last updated on 03/Dec/19

Answered by mr W last updated on 03/Dec/19

Commented by mr W last updated on 03/Dec/19
![(f/e)=(c/(a+b)) af=c×(c/(c+d))×e ⇒(f/e)=(c^2 /(a(c+d))) (c/(a+b))=(c^2 /(a(c+d))) ⇒(a/(a+b))=(c/(c+d)) ⇒(a/b)=(c/d)=k (1/2)[(((a+b)^2 f)/a)−af]=(((a+b)d)/3) ⇒f=((2(a+b)ad)/(3(2a+b)b))=((2k(k+1)d)/(3(2k+1))) ⇒e=((2(k+1)^2 b)/(3(2k+1))) (f/(a−e))=((c+d)/a) ⇒(((2k)/(3(2k+1)))/(k−((2(k+1)^2 )/(3(2k+1)))))=(1/k) ⇒2k^2 −k−2=0 ⇒k=((1+(√(17)))/4)≈1.28 (k/(k+1))=((1+(√(17)))/(5+(√(17))))=(((√(17))−3)/2)≈0.56 i.e. the ratio of side lengthes of the outer rectangle can be of any value. the condition is only (a/b)=(c/d)=((1+(√(17)))/4) or (a/(a+b))=(c/(c+d))=(((√(17))−3)/2)](https://www.tinkutara.com/question/Q74897.png)
$$\frac{{f}}{{e}}=\frac{{c}}{{a}+{b}} \\ $$$${af}={c}×\frac{{c}}{{c}+{d}}×{e} \\ $$$$\Rightarrow\frac{{f}}{{e}}=\frac{{c}^{\mathrm{2}} }{{a}\left({c}+{d}\right)} \\ $$$$\frac{{c}}{{a}+{b}}=\frac{{c}^{\mathrm{2}} }{{a}\left({c}+{d}\right)} \\ $$$$\Rightarrow\frac{{a}}{{a}+{b}}=\frac{{c}}{{c}+{d}} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{{c}}{{d}}={k} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\left({a}+{b}\right)^{\mathrm{2}} {f}}{{a}}−{af}\right]=\frac{\left({a}+{b}\right){d}}{\mathrm{3}} \\ $$$$\Rightarrow{f}=\frac{\mathrm{2}\left({a}+{b}\right){ad}}{\mathrm{3}\left(\mathrm{2}{a}+{b}\right){b}}=\frac{\mathrm{2}{k}\left({k}+\mathrm{1}\right){d}}{\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\Rightarrow{e}=\frac{\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} {b}}{\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\frac{{f}}{{a}−{e}}=\frac{{c}+{d}}{{a}} \\ $$$$\Rightarrow\frac{\frac{\mathrm{2}{k}}{\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)}}{{k}−\frac{\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)}}=\frac{\mathrm{1}}{{k}} \\ $$$$\Rightarrow\mathrm{2}{k}^{\mathrm{2}} −{k}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{4}}\approx\mathrm{1}.\mathrm{28} \\ $$$$\frac{{k}}{{k}+\mathrm{1}}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{5}+\sqrt{\mathrm{17}}}=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}}\approx\mathrm{0}.\mathrm{56} \\ $$$${i}.{e}.\:{the}\:{ratio}\:{of}\:{side}\:{lengthes}\:{of}\:{the} \\ $$$${outer}\:{rectangle}\:{can}\:{be}\:{of}\:{any}\:{value}. \\ $$$${the}\:{condition}\:{is}\:{only} \\ $$$$\frac{{a}}{{b}}=\frac{{c}}{{d}}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{4}} \\ $$$${or} \\ $$$$\frac{{a}}{{a}+{b}}=\frac{{c}}{{c}+{d}}=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 03/Dec/19

$${sir}\:{could}\:{i}\:{make}\:{the}\:{question} \\ $$$${clear}\:?\:\:{the}\:{small}\:{blue}\:{triangles} \\ $$$${have}\:{the}\:{same}\:{area}. \\ $$$${The}\:{four}\:{pink}\:{quadrilaterals} \\ $$$${and}\:{the}\:{central}\:{one}\:{have}\:{an} \\ $$$${equal}\:{other}\:{area}. \\ $$$${What}\:{is}\:{the}\:{ratio}\:{of}\:{length}\:{of} \\ $$$${the}\:{outer}\:{rectangle}\:{to}\:{its}\:{breadth}? \\ $$$$ \\ $$
Commented by mr W last updated on 04/Dec/19

$${thank}\:{you}\:{sir}\:{for}\:{clarifying}! \\ $$$${i}\:{have}\:{modified}\:{my}\:{answer}. \\ $$$${the}\:{ratio}\:{of}\:{lengthes}\:{of}\:{the}\:{rectangle} \\ $$$${can}\:{be}\:{of}\:{any}\:{value}.\:{but}\:{the}\:{sides}\: \\ $$$${must}\:{be}\:{divided}\:{with}\:{a}\:{certain}\:{ratio}. \\ $$
Commented by mr W last updated on 04/Dec/19

$${A}_{{red}} =\frac{\left({a}+{b}\right){d}}{\mathrm{3}}=\frac{\left({k}+\mathrm{1}\right){bd}}{\mathrm{3}} \\ $$$${A}_{{blue}} =\frac{{af}}{\mathrm{2}}=\frac{{k}^{\mathrm{2}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)}×\frac{\left({k}+\mathrm{1}\right){bd}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{A}_{{red}} }{{A}_{{blue}} }=\frac{\mathrm{2}{k}+\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\mathrm{3}\sqrt{\mathrm{17}}+\mathrm{5}}{\mathrm{8}}\approx\mathrm{2}.\mathrm{17} \\ $$$${i}.{e}.\:{the}\:{ratio}\:{of}\:{area}\:{of}\:{a}\:{blue}\:{triangle} \\ $$$${to}\:{that}\:{of}\:{a}\:{red}\:{zone}\:{is}\:{independent} \\ $$$${from}\:{the}\:{ratio}\:{of}\:{side}\:{lengthes}\:{of}\:{the} \\ $$$${outer}\:{rectangle}.\:\:{it}'{s}\:{not}\:{possible}\:{that} \\ $$$${a}\:{triangle}\:{area}\:{is}\:{equal}\:{to}\:{that}\:{of}\:{a} \\ $$$${red}\:{area}. \\ $$
Commented by mr W last updated on 04/Dec/19

Commented by mr W last updated on 04/Dec/19

Commented by mr W last updated on 04/Dec/19

Commented by mr W last updated on 04/Dec/19
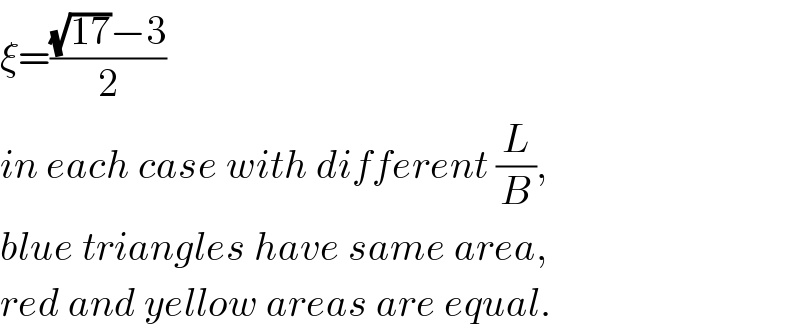
$$\xi=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}} \\ $$$${in}\:{each}\:{case}\:{with}\:{different}\:\frac{{L}}{{B}}, \\ $$$${blue}\:{triangles}\:{have}\:{same}\:{area}, \\ $$$${red}\:{and}\:{yellow}\:{areas}\:{are}\:{equal}. \\ $$
Commented by ajfour last updated on 04/Dec/19

$${Thanks}\:{sir},\:{totally}\:{convinced}. \\ $$$${can}\:{the}\:{blue},\:{yellow},\:{and}\:{red} \\ $$$${areas}\:{all}\:{be}\:{equal}\:{for}\:{certain} \\ $$$${side}\:{ratio}\:{of}\:{outer}\:{rectangle},\:{Sir}? \\ $$
