Question Number 74945 by chess1 last updated on 04/Dec/19

Commented by chess1 last updated on 04/Dec/19

$$\mathrm{solve}\:\mathrm{equation} \\ $$
Answered by MJS last updated on 04/Dec/19
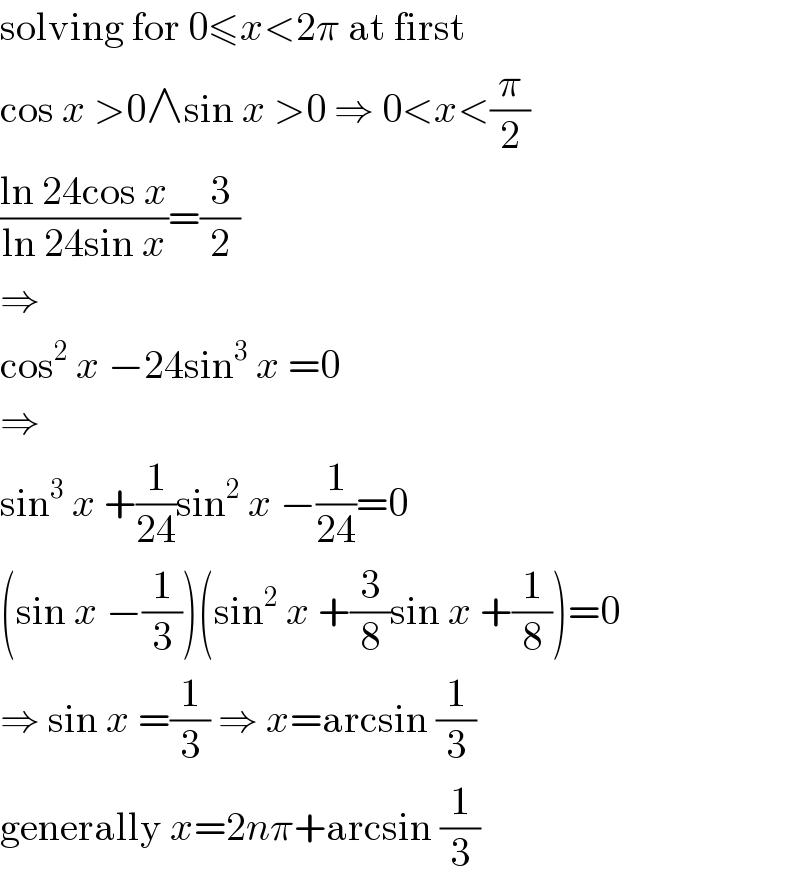
$$\mathrm{solving}\:\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\mathrm{at}\:\mathrm{first} \\ $$$$\mathrm{cos}\:{x}\:>\mathrm{0}\wedge\mathrm{sin}\:{x}\:>\mathrm{0}\:\Rightarrow\:\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\mathrm{ln}\:\mathrm{24cos}\:{x}}{\mathrm{ln}\:\mathrm{24sin}\:{x}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{24sin}^{\mathrm{3}} \:{x}\:=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{3}} \:{x}\:+\frac{\mathrm{1}}{\mathrm{24}}\mathrm{sin}^{\mathrm{2}} \:{x}\:−\frac{\mathrm{1}}{\mathrm{24}}=\mathrm{0} \\ $$$$\left(\mathrm{sin}\:{x}\:−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{sin}^{\mathrm{2}} \:{x}\:+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{sin}\:{x}\:+\frac{\mathrm{1}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{x}=\mathrm{arcsin}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{generally}\:{x}=\mathrm{2}{n}\pi+\mathrm{arcsin}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
