Question Number 74947 by chess1 last updated on 04/Dec/19

Answered by MJS last updated on 05/Dec/19
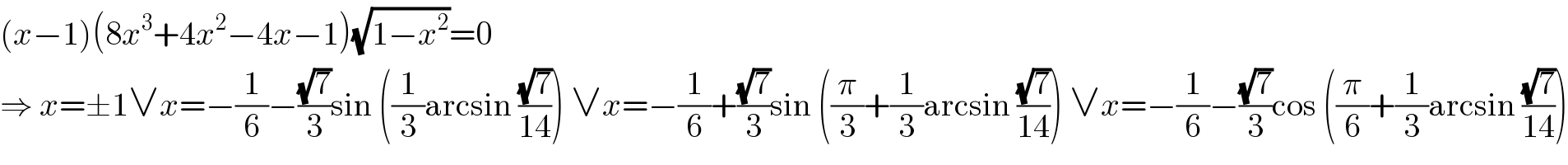
$$\left({x}−\mathrm{1}\right)\left(\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{1}\vee{x}=−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\:\vee{x}=−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\:\vee{x}=−\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right) \\ $$
Commented by chess1 last updated on 05/Dec/19

$$\mathrm{prove}\:\mathrm{that} \\ $$
Commented by MJS last updated on 05/Dec/19

$$\mathrm{no}\:\mathrm{need}\:\mathrm{to}\:\mathrm{prove},\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{solving}\:\mathrm{method} \\ $$
