Question Number 74978 by aliesam last updated on 05/Dec/19
Commented by aliesam last updated on 05/Dec/19
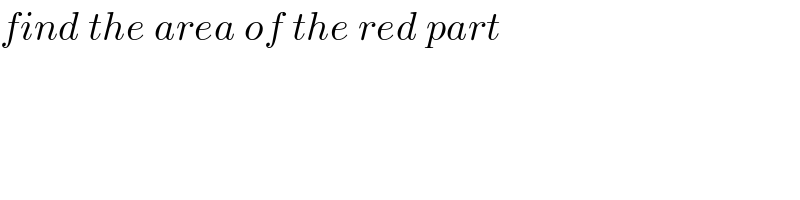
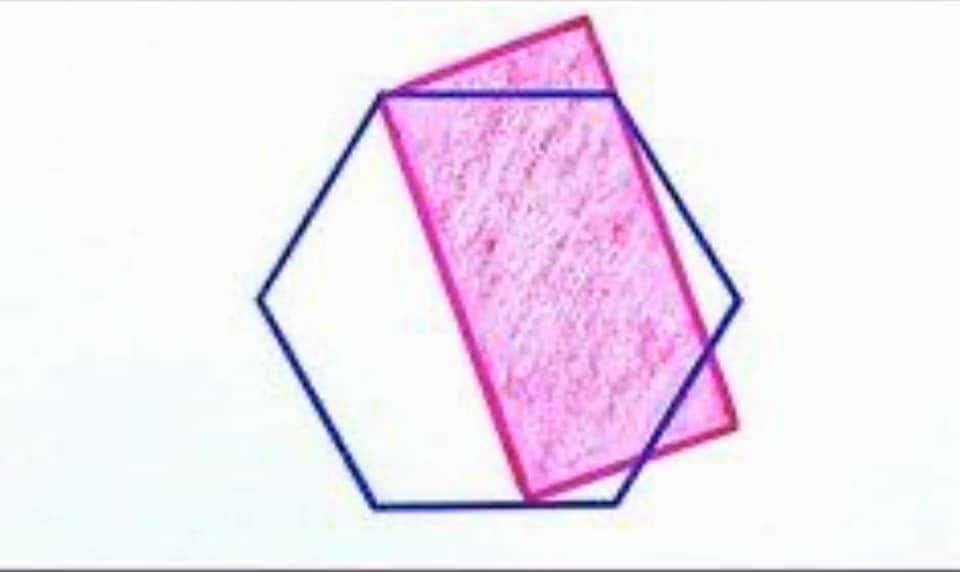
$${find}\:{the}\:{area}\:{of}\:{the}\:{red}\:{part} \\ $$
Answered by mind is power last updated on 05/Dec/19
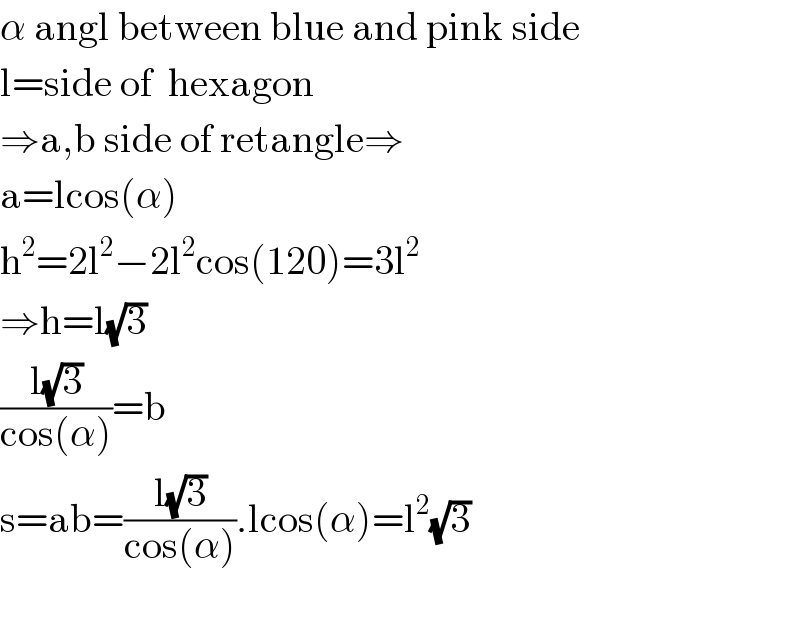
$$\alpha\:\mathrm{angl}\:\mathrm{between}\:\mathrm{blue}\:\mathrm{and}\:\mathrm{pink}\:\mathrm{side}\: \\ $$$$\mathrm{l}=\mathrm{side}\:\mathrm{of}\:\:\mathrm{hexagon} \\ $$$$\Rightarrow\mathrm{a},\mathrm{b}\:\mathrm{side}\:\mathrm{of}\:\mathrm{retangle}\Rightarrow \\ $$$$\mathrm{a}=\mathrm{lcos}\left(\alpha\right) \\ $$$$\mathrm{h}^{\mathrm{2}} =\mathrm{2l}^{\mathrm{2}} −\mathrm{2l}^{\mathrm{2}} \mathrm{cos}\left(\mathrm{120}\right)=\mathrm{3l}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{h}=\mathrm{l}\sqrt{\mathrm{3}} \\ $$$$\frac{\mathrm{l}\sqrt{\mathrm{3}}}{\mathrm{cos}\left(\alpha\right)}=\mathrm{b} \\ $$$$\mathrm{s}=\mathrm{ab}=\frac{\mathrm{l}\sqrt{\mathrm{3}}}{\mathrm{cos}\left(\alpha\right)}.\mathrm{lcos}\left(\alpha\right)=\mathrm{l}^{\mathrm{2}} \sqrt{\mathrm{3}} \\ $$$$ \\ $$
