Menu Close

Question-74994

Tinku Tara 0 Comments
Pin




Question Number 74994 by aliesam last updated on 05/Dec/19
Commented by mind is power last updated on 05/Dec/19
Commented by mind is power last updated on 05/Dec/19
∠ACB=α,∠ABC=β,∠BAC=ϕ AB=c,BC=a,AC=b OL=OT=r_3 ⇒MLOT Squar ⇒MT=r_3 =r OBS≡OBT ⇒∠OBC=(1/2)∠(MBC) ∠MBC=180−(90+α)=90−α ⇒∠OBS=∠OBC=((90−α)/2)=(π/4)−(α/2)(i prefer radian ) BM=asin(α) BT=asin(α)+r BO=(r/(sin((π/4)−(α/2)))),BO^2 =(r^2 /(sin^2 ((π/4)−(α/2))))=(r^2 /((((√2)/2)cos((α/2))−((√2)/2)sin((α/2)))^2 )) =((2r^2 )/(1−sin(α))) BO^2 =BT^2 +r^2 =(asin(α)+r)^2 +r^2 =((2r^2 )/(1−sin(α))) ⇔2r^2 +2arsin(α)+a^2 sin^2 (α)=((2r^2 )/(1−sin(α))) ⇔((−2r^2 sin(α))/(1−sin(α)))+2arsin(α)+a^2 sin^2 (α)=0 ⇔−2r^2 +2a(1−sin(α)r+a^2 sin(α)(1−sinα)=0 Δ=4a^2 (1−sinα)^2 +8a^2 sin(α)(1−sin(α)) =4a^2 (1+sin^2 (α)−2sin(α)+2sin(α)−2sin^2 (α)) =4a^2 (1−sin^2 (α))=4a^2 cos^2 (α) r=((−2a(1−sin(α))−2acos(α))/(−4)) =((a(cos(α)−sin(α)+1))/2)=r_3 sam idea Symetric approche r_4 =((c(cos(ϕ)−sin(ϕ)+1))/2),r_5 =((b(cos(ϕ)−sin(ϕ)+1))/2) r_6 =((a(cos(β)−sin(β)+1))/2),r_2 =((b(cos(α)−sin(α)+1))/2) r_1 =((c(cos(β)−sin(β)+1))/2) r_1 .r_3 r_5 =((abc(cos(β)−sin(β)+1)(cos(α)−sin(α)+1)(cos(ϕ)−sin(ϕ)+1))/8) r_2 r_4 r_6 =((abc(cos(β)−sin(β)+1)(cos(α)−sin(α)+1)(cos(ϕ)−sin(ϕ)+1))/8) ⇔r_1 .r_3 .r_5 =r_2 .r_4 .r_6
$$\angle\mathrm{ACB}=\alpha,\angle\mathrm{ABC}=\beta,\angle\mathrm{BAC}=\varphi \\ $$$$\mathrm{AB}=\mathrm{c},\mathrm{BC}=\mathrm{a},\mathrm{AC}=\mathrm{b} \\ $$$$\mathrm{OL}=\mathrm{OT}=\mathrm{r}_{\mathrm{3}} \:\Rightarrow\mathrm{MLOT}\:\mathrm{Squar} \\ $$$$\Rightarrow\mathrm{MT}=\mathrm{r}_{\mathrm{3}} =\mathrm{r} \\ $$$$\mathrm{OBS}\equiv\mathrm{OBT} \\ $$$$\Rightarrow\angle\mathrm{OBC}=\frac{\mathrm{1}}{\mathrm{2}}\angle\left(\mathrm{MBC}\right) \\ $$$$\angle\mathrm{MBC}=\mathrm{180}−\left(\mathrm{90}+\alpha\right)=\mathrm{90}−\alpha \\ $$$$\Rightarrow\angle\mathrm{OBS}=\angle\mathrm{OBC}=\frac{\mathrm{90}−\alpha}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\left(\mathrm{i}\:\mathrm{prefer}\:\mathrm{radian}\:\right) \\ $$$$\mathrm{BM}=\mathrm{asin}\left(\alpha\right) \\ $$$$\mathrm{BT}=\mathrm{asin}\left(\alpha\right)+\mathrm{r} \\ $$$$\mathrm{BO}=\frac{\mathrm{r}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)},\mathrm{BO}^{\mathrm{2}} =\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)}=\frac{\mathrm{r}^{\mathrm{2}} }{\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}}\right)\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2r}^{\mathrm{2}} }{\mathrm{1}−\mathrm{sin}\left(\alpha\right)} \\ $$$$\mathrm{BO}^{\mathrm{2}} =\mathrm{BT}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\left(\mathrm{asin}\left(\alpha\right)+\mathrm{r}\right)^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} =\frac{\mathrm{2r}^{\mathrm{2}} }{\mathrm{1}−\mathrm{sin}\left(\alpha\right)} \\ $$$$\Leftrightarrow\mathrm{2r}^{\mathrm{2}} +\mathrm{2arsin}\left(\alpha\right)+\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\alpha\right)=\frac{\mathrm{2r}^{\mathrm{2}} }{\mathrm{1}−\mathrm{sin}\left(\alpha\right)} \\ $$$$\Leftrightarrow\frac{−\mathrm{2r}^{\mathrm{2}} \mathrm{sin}\left(\alpha\right)}{\mathrm{1}−\mathrm{sin}\left(\alpha\right)}+\mathrm{2arsin}\left(\alpha\right)+\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\alpha\right)=\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{2r}^{\mathrm{2}} +\mathrm{2a}\left(\mathrm{1}−\mathrm{sin}\left(\alpha\right)\mathrm{r}+\mathrm{a}^{\mathrm{2}} \mathrm{sin}\left(\alpha\right)\left(\mathrm{1}−\mathrm{sin}\alpha\right)=\mathrm{0}\right. \\ $$$$\Delta=\mathrm{4a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\alpha\right)^{\mathrm{2}} +\mathrm{8a}^{\mathrm{2}} \mathrm{sin}\left(\alpha\right)\left(\mathrm{1}−\mathrm{sin}\left(\alpha\right)\right) \\ $$$$=\mathrm{4a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left(\alpha\right)−\mathrm{2sin}\left(\alpha\right)+\mathrm{2sin}\left(\alpha\right)−\mathrm{2sin}^{\mathrm{2}} \left(\alpha\right)\right) \\ $$$$=\mathrm{4a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\alpha\right)\right)=\mathrm{4a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \left(\alpha\right) \\ $$$$\mathrm{r}=\frac{−\mathrm{2a}\left(\mathrm{1}−\mathrm{sin}\left(\alpha\right)\right)−\mathrm{2acos}\left(\alpha\right)}{−\mathrm{4}} \\ $$$$=\frac{\mathrm{a}\left(\mathrm{cos}\left(\alpha\right)−\mathrm{sin}\left(\alpha\right)+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{r}_{\mathrm{3}} \\ $$$$\mathrm{sam}\:\:\mathrm{idea}\:\mathrm{Symetric}\:\mathrm{approche} \\ $$$$\mathrm{r}_{\mathrm{4}} =\frac{\mathrm{c}\left(\mathrm{cos}\left(\varphi\right)−\mathrm{sin}\left(\varphi\right)+\mathrm{1}\right)}{\mathrm{2}},\mathrm{r}_{\mathrm{5}} =\frac{\mathrm{b}\left(\mathrm{cos}\left(\varphi\right)−\mathrm{sin}\left(\varphi\right)+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{r}_{\mathrm{6}} =\frac{\mathrm{a}\left(\mathrm{cos}\left(\beta\right)−\mathrm{sin}\left(\beta\right)+\mathrm{1}\right)}{\mathrm{2}},\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{b}\left(\mathrm{cos}\left(\alpha\right)−\mathrm{sin}\left(\alpha\right)+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{c}\left(\mathrm{cos}\left(\beta\right)−\mathrm{sin}\left(\beta\right)+\mathrm{1}\right)}{\mathrm{2}}\: \\ $$$$\mathrm{r}_{\mathrm{1}} .\mathrm{r}_{\mathrm{3}} \mathrm{r}_{\mathrm{5}} =\frac{\mathrm{abc}\left(\mathrm{cos}\left(\beta\right)−\mathrm{sin}\left(\beta\right)+\mathrm{1}\right)\left(\mathrm{cos}\left(\alpha\right)−\mathrm{sin}\left(\alpha\right)+\mathrm{1}\right)\left(\mathrm{cos}\left(\varphi\right)−\mathrm{sin}\left(\varphi\right)+\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\mathrm{r}_{\mathrm{2}} \mathrm{r}_{\mathrm{4}} \mathrm{r}_{\mathrm{6}} =\frac{\mathrm{abc}\left(\mathrm{cos}\left(\beta\right)−\mathrm{sin}\left(\beta\right)+\mathrm{1}\right)\left(\mathrm{cos}\left(\alpha\right)−\mathrm{sin}\left(\alpha\right)+\mathrm{1}\right)\left(\mathrm{cos}\left(\varphi\right)−\mathrm{sin}\left(\varphi\right)+\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\Leftrightarrow{r}_{\mathrm{1}} .{r}_{\mathrm{3}} .{r}_{\mathrm{5}} ={r}_{\mathrm{2}} .{r}_{\mathrm{4}} .{r}_{\mathrm{6}} \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 05/Dec/19
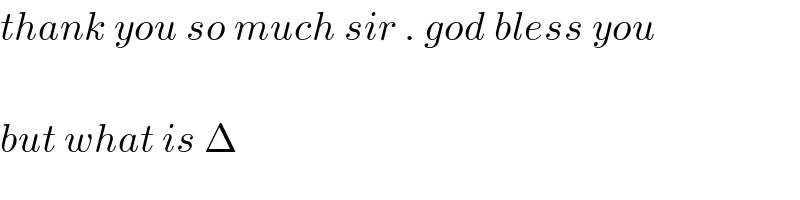
thank you so much sir . god bless you but what is Δ
$${thank}\:{you}\:{so}\:{much}\:{sir}\:.\:{god}\:{bless}\:{you} \\ $$$$ \\ $$$${but}\:{what}\:{is}\:\Delta\: \\ $$
Commented by mind is power last updated on 05/Dec/19
in Franc we use Δ discriminant of aX^2 +bX+c :Δ=b^2 −4ac
$$\mathrm{in}\:\mathrm{Franc}\:\:\mathrm{we}\:\mathrm{use}\:\Delta\:\mathrm{discriminant}\:\mathrm{of}\:\mathrm{aX}^{\mathrm{2}} +\mathrm{bX}+\mathrm{c} \\ $$$$:\Delta=\mathrm{b}^{\mathrm{2}} −\mathrm{4ac}\: \\ $$
Commented by aliesam last updated on 05/Dec/19
thank you sir
$${thank}\:{you}\:{sir}\: \\ $$
Commented by mind is power last updated on 05/Dec/19
y′re Welcom
$$\mathrm{y}'\mathrm{re}\:\mathrm{Welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *