Question-75136

Question Number 75136 by chess1 last updated on 07/Dec/19

Commented by MJS last updated on 07/Dec/19

$$\frac{\mathrm{1}}{\mathrm{10}} \\ $$

Commented by mathmax by abdo last updated on 07/Dec/19

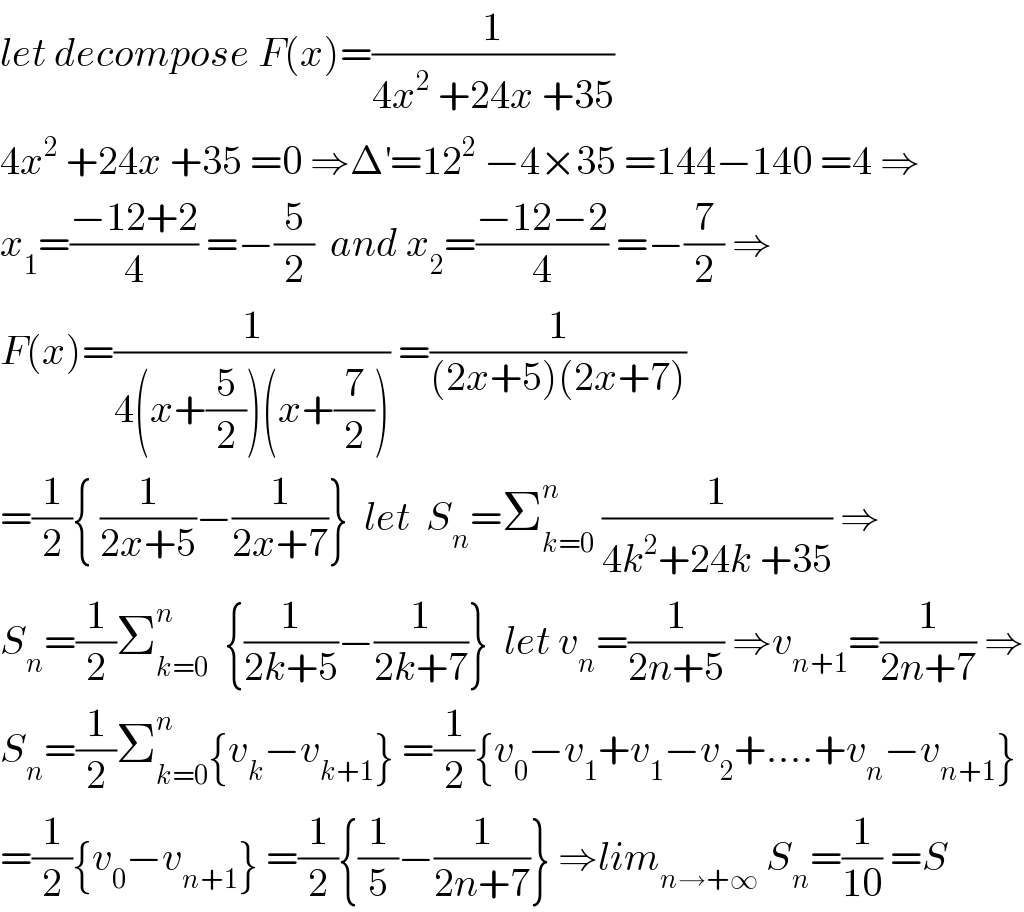
let decompose F(x)=(1/(4x^2 +24x +35)) 4x^2 +24x +35 =0 ⇒Δ^′ =12^2 −4×35 =144−140 =4 ⇒ x_1 =((−12+2)/4) =−(5/2) and x_2 =((−12−2)/4) =−(7/2) ⇒ F(x)=(1/(4(x+(5/2))(x+(7/2)))) =(1/((2x+5)(2x+7))) =(1/2){ (1/(2x+5))−(1/(2x+7))} let S_n =Σ_(k=0) ^n (1/(4k^2 +24k +35)) ⇒ S_n =(1/2)Σ_(k=0) ^n {(1/(2k+5))−(1/(2k+7))} let v_n =(1/(2n+5)) ⇒v_(n+1) =(1/(2n+7)) ⇒ S_n =(1/2)Σ_(k=0) ^n {v_k −v_(k+1) } =(1/2){v_0 −v_1 +v_1 −v_2 +....+v_n −v_(n+1) } =(1/2){v_0 −v_(n+1) } =(1/2){(1/5)−(1/(2n+7))} ⇒lim_(n→+∞) S_n =(1/(10)) =S

$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{24}{x}\:+\mathrm{35}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{24}{x}\:+\mathrm{35}\:=\mathrm{0}\:\Rightarrow\Delta^{'} =\mathrm{12}^{\mathrm{2}} \:−\mathrm{4}×\mathrm{35}\:=\mathrm{144}−\mathrm{140}\:=\mathrm{4}\:\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{−\mathrm{12}+\mathrm{2}}{\mathrm{4}}\:=−\frac{\mathrm{5}}{\mathrm{2}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{12}−\mathrm{2}}{\mathrm{4}}\:=−\frac{\mathrm{7}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\left({x}+\frac{\mathrm{5}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{7}}{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{5}\right)\left(\mathrm{2}{x}+\mathrm{7}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{7}}\right\}\:\:{let}\:\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{24}{k}\:+\mathrm{35}}\:\Rightarrow \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\left\{\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{7}}\right\}\:\:{let}\:{v}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{5}}\:\Rightarrow{v}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{7}}\:\Rightarrow \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}} \left\{{v}_{{k}} −{v}_{{k}+\mathrm{1}} \right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{{v}_{\mathrm{0}} −{v}_{\mathrm{1}} +{v}_{\mathrm{1}} −{v}_{\mathrm{2}} +….+{v}_{{n}} −{v}_{{n}+\mathrm{1}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{v}_{\mathrm{0}} −{v}_{{n}+\mathrm{1}} \right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{7}}\right\}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{10}}\:={S} \\ $$

Commented by chess1 last updated on 08/Dec/19

$$\mathrm{thanks} \\ $$

Answered by 21042004 last updated on 13/Dec/19

$$\mathrm{0}.\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply