Question-75158

Question Number 75158 by peter frank last updated on 08/Dec/19

Answered by mr W last updated on 08/Dec/19

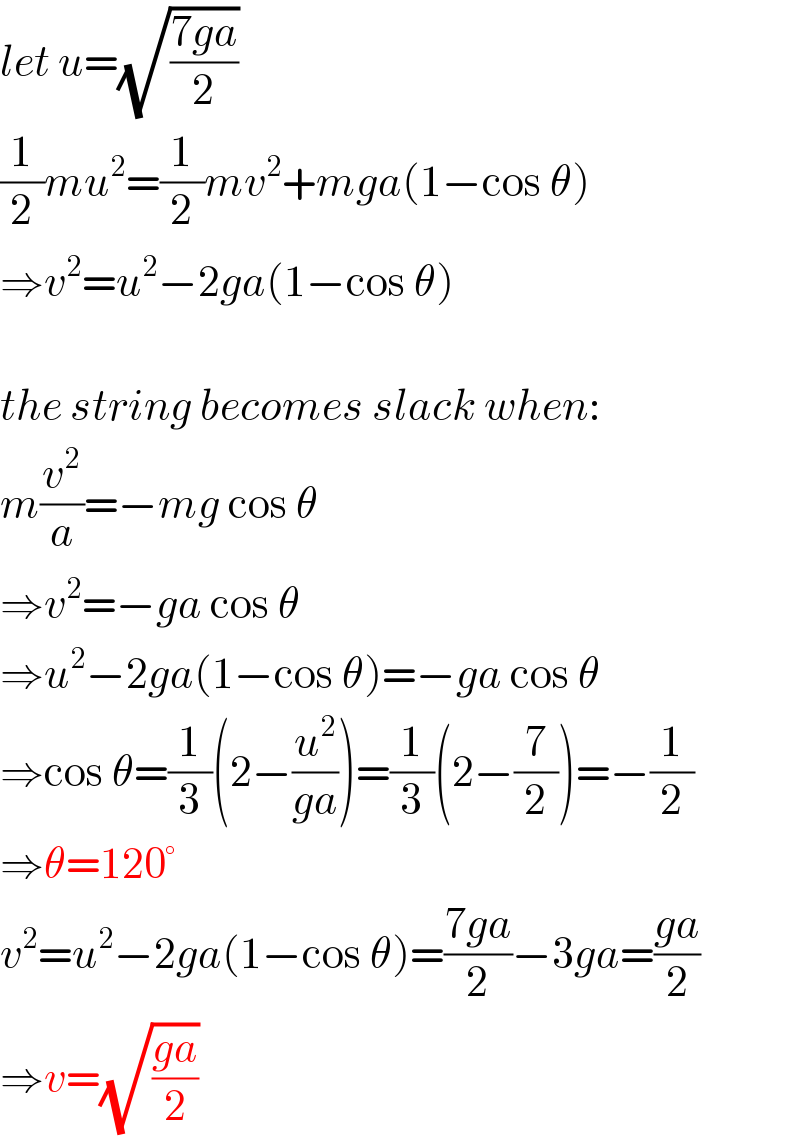
let u=(√((7ga)/2)) (1/2)mu^2 =(1/2)mv^2 +mga(1−cos θ) ⇒v^2 =u^2 −2ga(1−cos θ) the string becomes slack when: m(v^2 /a)=−mg cos θ ⇒v^2 =−ga cos θ ⇒u^2 −2ga(1−cos θ)=−ga cos θ ⇒cos θ=(1/3)(2−(u^2 /(ga)))=(1/3)(2−(7/2))=−(1/2) ⇒θ=120° v^2 =u^2 −2ga(1−cos θ)=((7ga)/2)−3ga=((ga)/2) ⇒v=(√((ga)/2))

$${let}\:{u}=\sqrt{\frac{\mathrm{7}{ga}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mu}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +{mga}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow{v}^{\mathrm{2}} ={u}^{\mathrm{2}} −\mathrm{2}{ga}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$ \\ $$$${the}\:{string}\:{becomes}\:{slack}\:{when}: \\ $$$${m}\frac{{v}^{\mathrm{2}} }{{a}}=−{mg}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{v}^{\mathrm{2}} =−{ga}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{u}^{\mathrm{2}} −\mathrm{2}{ga}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=−{ga}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}−\frac{{u}^{\mathrm{2}} }{{ga}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}−\frac{\mathrm{7}}{\mathrm{2}}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{120}° \\ $$$${v}^{\mathrm{2}} ={u}^{\mathrm{2}} −\mathrm{2}{ga}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\frac{\mathrm{7}{ga}}{\mathrm{2}}−\mathrm{3}{ga}=\frac{{ga}}{\mathrm{2}} \\ $$$$\Rightarrow{v}=\sqrt{\frac{{ga}}{\mathrm{2}}} \\ $$

Commented by peter frank last updated on 08/Dec/19

$${thank}\:{very}\:{much} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply