Question Number 75173 by liki last updated on 08/Dec/19
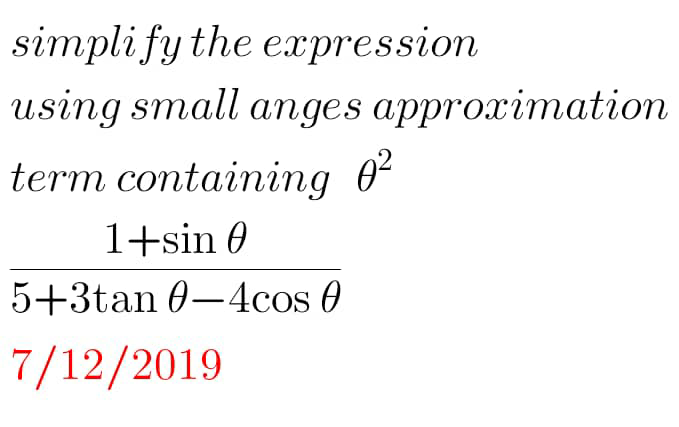
Commented by liki last updated on 08/Dec/19

$$…{i}\:{need}\:{help}\:{plz} \\ $$
Answered by mind is power last updated on 08/Dec/19
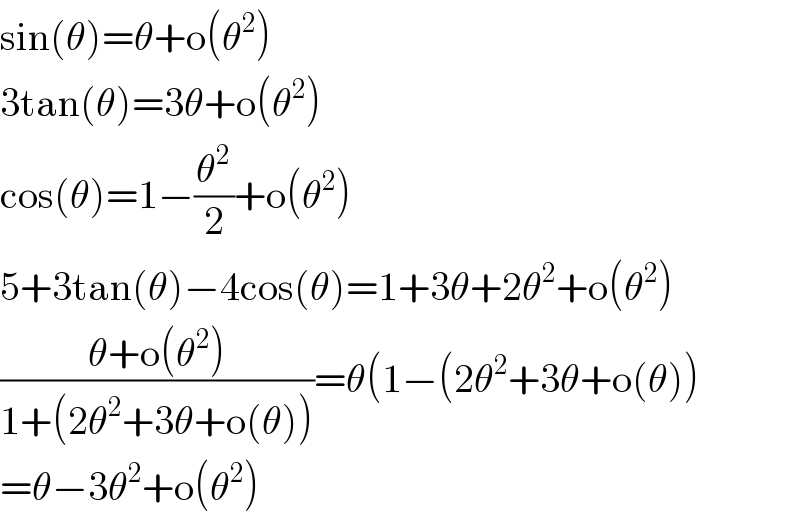
$$\mathrm{sin}\left(\theta\right)=\theta+\mathrm{o}\left(\theta^{\mathrm{2}} \right) \\ $$$$\mathrm{3tan}\left(\theta\right)=\mathrm{3}\theta+\mathrm{o}\left(\theta^{\mathrm{2}} \right) \\ $$$$\mathrm{cos}\left(\theta\right)=\mathrm{1}−\frac{\theta^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\theta^{\mathrm{2}} \right) \\ $$$$\mathrm{5}+\mathrm{3tan}\left(\theta\right)−\mathrm{4cos}\left(\theta\right)=\mathrm{1}+\mathrm{3}\theta+\mathrm{2}\theta^{\mathrm{2}} +\mathrm{o}\left(\theta^{\mathrm{2}} \right) \\ $$$$\frac{\theta+\mathrm{o}\left(\theta^{\mathrm{2}} \right)}{\mathrm{1}+\left(\mathrm{2}\theta^{\mathrm{2}} +\mathrm{3}\theta+\mathrm{o}\left(\theta\right)\right)}=\theta\left(\mathrm{1}−\left(\mathrm{2}\theta^{\mathrm{2}} +\mathrm{3}\theta+\mathrm{o}\left(\theta\right)\right)\right. \\ $$$$=\theta−\mathrm{3}\theta^{\mathrm{2}} +\mathrm{o}\left(\theta^{\mathrm{2}} \right) \\ $$
Commented by liki last updated on 08/Dec/19

$$…{thank}\:{you}\:{sir}. \\ $$
