Menu Close

Question-75177

Tinku Tara 0 Comments
Pin




Question Number 75177 by chess1 last updated on 08/Dec/19
Commented by chess1 last updated on 08/Dec/19
sir mind is power please solution
$$\mathrm{sir}\:\mathrm{mind}\:\mathrm{is}\:\mathrm{power}\:\:\mathrm{please}\:\mathrm{solution} \\ $$
Commented by mind is power last updated on 08/Dec/19
sir please dont dealt this Quation! i spend 1 hour to find how to solve this i found i general why to go throw withe m∈N^∗ ∫((sin^m (x))/( (√(sin(x)))))dx
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{dont}\:\mathrm{dealt}\:\mathrm{this}\:\mathrm{Quation}! \\ $$$$\mathrm{i}\:\mathrm{spend}\:\mathrm{1}\:\mathrm{hour}\:\mathrm{to}\:\mathrm{find}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\mathrm{i}\:\mathrm{found} \\ $$$$\mathrm{i}\:\mathrm{general}\:\mathrm{why}\:\mathrm{to}\:\mathrm{go}\:\mathrm{throw}\:\mathrm{withe}\:\mathrm{m}\in\mathbb{N}^{\ast} \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{m}} \left(\mathrm{x}\right)}{\:\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}}\mathrm{dx} \\ $$
Answered by mind is power last updated on 08/Dec/19
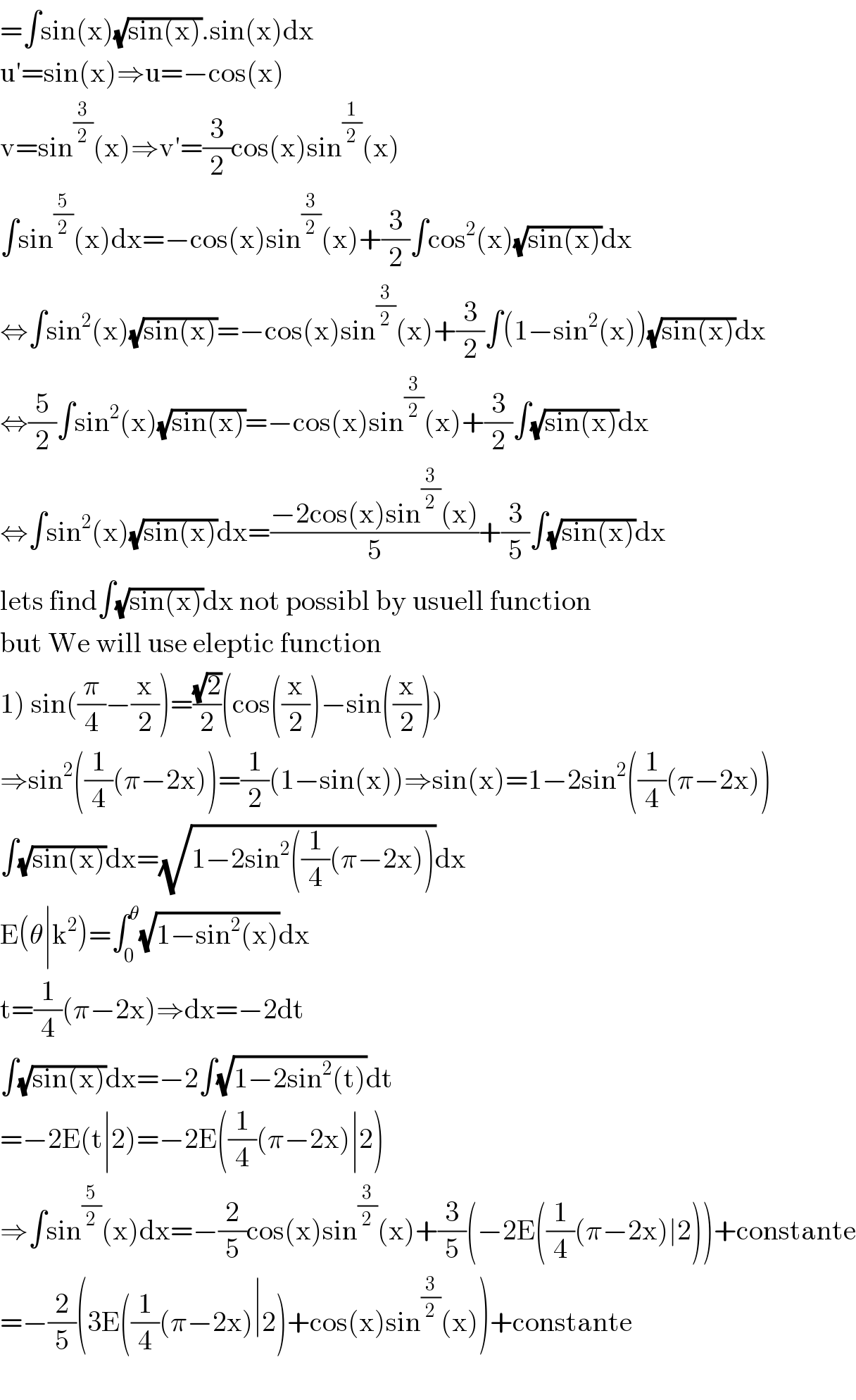
=∫sin(x)(√(sin(x))).sin(x)dx u′=sin(x)⇒u=−cos(x) v=sin^(3/2) (x)⇒v′=(3/2)cos(x)sin^(1/2) (x) ∫sin^(5/2) (x)dx=−cos(x)sin^(3/2) (x)+(3/2)∫cos^2 (x)(√(sin(x)))dx ⇔∫sin^2 (x)(√(sin(x)))=−cos(x)sin^(3/2) (x)+(3/2)∫(1−sin^2 (x))(√(sin(x)))dx ⇔(5/2)∫sin^2 (x)(√(sin(x)))=−cos(x)sin^(3/2) (x)+(3/2)∫(√(sin(x)))dx ⇔∫sin^2 (x)(√(sin(x)))dx=((−2cos(x)sin^(3/2) (x))/5)+(3/5)∫(√(sin(x)))dx lets find∫(√(sin(x)))dx not possibl by usuell function but We will use eleptic function 1) sin((π/4)−(x/2))=((√2)/2)(cos((x/2))−sin((x/2))) ⇒sin^2 ((1/4)(π−2x))=(1/2)(1−sin(x))⇒sin(x)=1−2sin^2 ((1/4)(π−2x)) ∫(√(sin(x)))dx=(√(1−2sin^2 ((1/4)(π−2x))))dx E(θ∣k^2 )=∫_0 ^θ (√(1−sin^2 (x)))dx t=(1/4)(π−2x)⇒dx=−2dt ∫(√(sin(x)))dx=−2∫(√(1−2sin^2 (t)))dt =−2E(t∣2)=−2E((1/4)(π−2x)∣2) ⇒∫sin^(5/2) (x)dx=−(2/5)cos(x)sin^(3/2) (x)+(3/5)(−2E((1/4)(π−2x)∣2))+constante =−(2/5)(3E((1/4)(π−2x)∣2)+cos(x)sin^(3/2) (x))+constante
$$=\int\mathrm{sin}\left(\mathrm{x}\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}.\mathrm{sin}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{u}'=\mathrm{sin}\left(\mathrm{x}\right)\Rightarrow\mathrm{u}=−\mathrm{cos}\left(\mathrm{x}\right) \\ $$$$\mathrm{v}=\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)\Rightarrow\mathrm{v}'=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{x}\right) \\ $$$$\int\mathrm{sin}^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\mathrm{x}\right)\mathrm{dx}=−\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)+\frac{\mathrm{3}}{\mathrm{2}}\int\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\Leftrightarrow\int\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}=−\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)+\frac{\mathrm{3}}{\mathrm{2}}\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\Leftrightarrow\frac{\mathrm{5}}{\mathrm{2}}\int\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}=−\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)+\frac{\mathrm{3}}{\mathrm{2}}\int\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\Leftrightarrow\int\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx}=\frac{−\mathrm{2cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{5}}\int\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\mathrm{lets}\:\mathrm{find}\int\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx}\:\mathrm{not}\:\mathrm{possibl}\:\mathrm{by}\:\mathrm{usuell}\:\mathrm{function} \\ $$$$\mathrm{but}\:\mathrm{We}\:\mathrm{will}\:\mathrm{use}\:\mathrm{eleptic}\:\mathrm{function} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{sin}\left(\mathrm{x}\right)\right)\Rightarrow\mathrm{sin}\left(\mathrm{x}\right)=\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\right) \\ $$$$\int\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx}=\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\right)}\mathrm{dx} \\ $$$$\mathrm{E}\left(\theta\mid\mathrm{k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\theta} \sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\Rightarrow\mathrm{dx}=−\mathrm{2dt} \\ $$$$\int\sqrt{\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{dx}=−\mathrm{2}\int\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \left(\mathrm{t}\right)}\mathrm{dt} \\ $$$$=−\mathrm{2E}\left(\mathrm{t}\mid\mathrm{2}\right)=−\mathrm{2E}\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\mid\mathrm{2}\right) \\ $$$$\Rightarrow\int\mathrm{sin}^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\mathrm{x}\right)\mathrm{dx}=−\frac{\mathrm{2}}{\mathrm{5}}\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)+\frac{\mathrm{3}}{\mathrm{5}}\left(−\mathrm{2E}\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\mid\mathrm{2}\right)\right)+\mathrm{constante} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{3E}\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2x}\right)\mid\mathrm{2}\right)+\mathrm{cos}\left(\mathrm{x}\right)\mathrm{sin}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{x}\right)\right)+\mathrm{constante} \\ $$$$ \\ $$
Commented by chess1 last updated on 09/Dec/19
great!
$$\mathrm{great}! \\ $$
Answered by aliesam last updated on 13/Dec/19

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *