Question-75230

Question Number 75230 by aliesam last updated on 08/Dec/19

Commented by mathmax by abdo last updated on 08/Dec/19

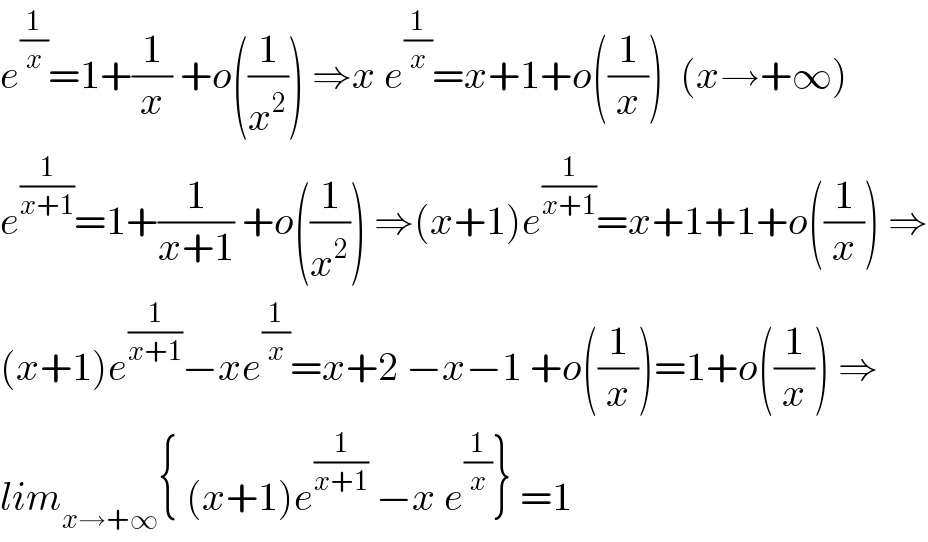
e^(1/x) =1+(1/x) +o((1/x^2 )) ⇒x e^(1/x) =x+1+o((1/x)) (x→+∞) e^(1/(x+1)) =1+(1/(x+1)) +o((1/x^2 )) ⇒(x+1)e^(1/(x+1)) =x+1+1+o((1/x)) ⇒ (x+1)e^(1/(x+1)) −xe^(1/x) =x+2 −x−1 +o((1/x))=1+o((1/x)) ⇒ lim_(x→+∞) { (x+1)e^(1/(x+1)) −x e^(1/x) } =1

$${e}^{\frac{\mathrm{1}}{{x}}} =\mathrm{1}+\frac{\mathrm{1}}{{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow{x}\:{e}^{\frac{\mathrm{1}}{{x}}} ={x}+\mathrm{1}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\:\:\left({x}\rightarrow+\infty\right) \\ $$$${e}^{\frac{\mathrm{1}}{{x}+\mathrm{1}}} =\mathrm{1}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow\left({x}+\mathrm{1}\right){e}^{\frac{\mathrm{1}}{{x}+\mathrm{1}}} ={x}+\mathrm{1}+\mathrm{1}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$$\left({x}+\mathrm{1}\right){e}^{\frac{\mathrm{1}}{{x}+\mathrm{1}}} −{xe}^{\frac{\mathrm{1}}{{x}}} ={x}+\mathrm{2}\:−{x}−\mathrm{1}\:+{o}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}+{o}\left(\frac{\mathrm{1}}{{x}}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \left\{\:\left({x}+\mathrm{1}\right){e}^{\frac{\mathrm{1}}{{x}+\mathrm{1}}} \:−{x}\:{e}^{\frac{\mathrm{1}}{{x}}} \right\}\:=\mathrm{1} \\ $$

Answered by mind is power last updated on 08/Dec/19

let f(z)=ze^(1/z) by mean value theorem ∃c∈]x,x+1[ f(x+1)−f(x)=f′(c) f′(c)=e^(1/c) −(e^(1/c) /c) since c>x⇒x→+∞,c→+∞ f′(c)→1 ⇒lim((x+1)e^(1/(x+1)) −xe^(1/x) )→1

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{ze}^{\frac{\mathrm{1}}{\mathrm{z}}} \\ $$$${by}\:{mean}\:{value}\:{theorem} \\ $$$$\left.\exists\mathrm{c}\in\right]\mathrm{x},\mathrm{x}+\mathrm{1}\left[\right. \\ $$$$\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}'\left(\mathrm{c}\right) \\ $$$$\mathrm{f}'\left(\mathrm{c}\right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{c}}} −\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{c}}} }{\mathrm{c}} \\ $$$$\mathrm{since}\:\mathrm{c}>\mathrm{x}\Rightarrow\mathrm{x}\rightarrow+\infty,\mathrm{c}\rightarrow+\infty \\ $$$$\mathrm{f}'\left(\mathrm{c}\right)\rightarrow\mathrm{1} \\ $$$$\Rightarrow\mathrm{lim}\left(\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}} −\mathrm{xe}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\rightarrow\mathrm{1} \\ $$

Commented by aliesam last updated on 08/Dec/19

$${thank}\:{you}\:{sir}\: \\ $$

Commented by mind is power last updated on 08/Dec/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply