Question Number 75248 by cesar.marval.larez@gmail.com last updated on 08/Dec/19

Commented by mathmax by abdo last updated on 14/Dec/19
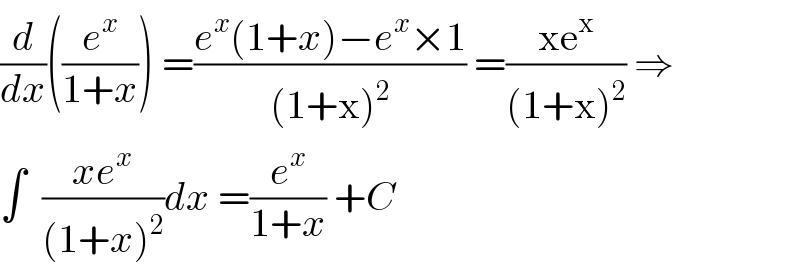
$$\frac{{d}}{{dx}}\left(\frac{{e}^{{x}} }{\mathrm{1}+{x}}\right)\:=\frac{{e}^{{x}} \left(\mathrm{1}+{x}\right)−{e}^{{x}} ×\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\:=\frac{\mathrm{xe}^{\mathrm{x}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\:\frac{{xe}^{{x}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}\:=\frac{{e}^{{x}} }{\mathrm{1}+{x}}\:+{C} \\ $$
Answered by mind is power last updated on 08/Dec/19
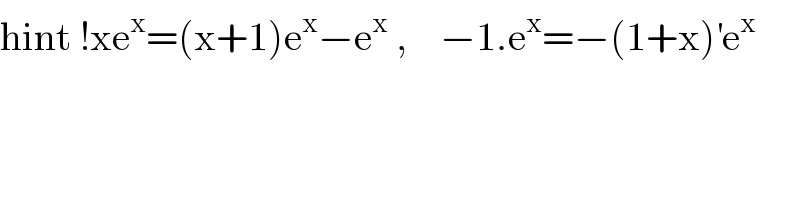
$$\mathrm{hint}\:!\mathrm{xe}^{\mathrm{x}} =\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} \:,\:\:\:\:−\mathrm{1}.\mathrm{e}^{\mathrm{x}} =−\left(\mathrm{1}+\mathrm{x}\right)^{'} \mathrm{e}^{\mathrm{x}} \\ $$$$ \\ $$
