Question Number 75291 by 21042004 last updated on 09/Dec/19
Answered by mind is power last updated on 09/Dec/19

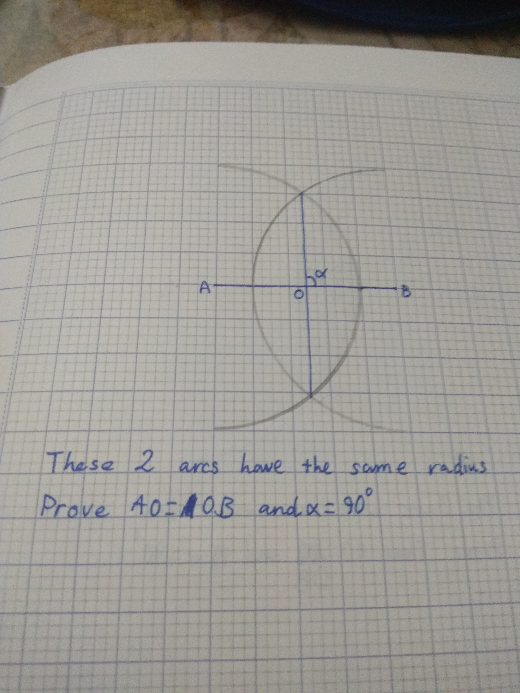
$$\mathrm{let}\:\mathrm{A}\left(\mathrm{a},\mathrm{0}\right),\mathrm{B}=\left(\mathrm{b},\mathrm{0}\right) \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{circl}\:\mathrm{center}\:\mathrm{in}\:\mathrm{A} \\ $$$$\mathrm{condition}\:\mathrm{3}\:\:\:\:\mathrm{AB}<\mathrm{2R} \\ $$$$\mathrm{if}\:\mathrm{not}\:\mathrm{C}_{\mathrm{A}} \cap\mathrm{C}_{\mathrm{B}} =\varnothing \\ $$$$\left(\mathrm{x}−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} ….\mathrm{C}_{\mathrm{A}} \\ $$$$\left(\mathrm{x}−\mathrm{b}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} …\mathrm{C}_{\mathrm{B}} \\ $$$$\mathrm{C}_{\mathrm{A}} \cap\mathrm{C}_{\mathrm{B}} \Leftrightarrow\left(\mathrm{x}−\mathrm{b}\right)^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{a}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} −\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \Rightarrow\mathrm{y}=\underset{−} {+}\sqrt{\mathrm{R}^{\mathrm{2}} −\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} }=\underset{−} {+}\sqrt{\alpha} \\ $$$$\mathrm{C}_{\mathrm{A}} \cap\mathrm{C}_{\mathrm{B}} =\left\{\mathrm{S},\mathrm{D}\right\}\:\mathrm{S}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}},\sqrt{}\alpha\right),\mathrm{D}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}},−\sqrt{}\alpha\right) \\ $$$$\mathrm{O}=\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}},\mathrm{0}\right) \\ $$$$\mid\mathrm{OA}\mid=\mid\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\mid=\mid\mathrm{OB}\mid=\mid\frac{\mathrm{b}−\mathrm{a}}{\mathrm{2}}\mid \\ $$$$\mathrm{OA}^{\mathrm{2}} +\mathrm{OS}^{\mathrm{2}} =\alpha+=\mathrm{R}^{\mathrm{2}} =\mathrm{AS}^{\mathrm{2}} \Rightarrow\mathrm{AOS}\:\mathrm{is}\:\mathrm{rectangle}\:\mathrm{in}\:\mathrm{O}\:\mathrm{pythagor}\:\mathrm{theorem} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
