Question Number 75296 by ajfour last updated on 09/Dec/19
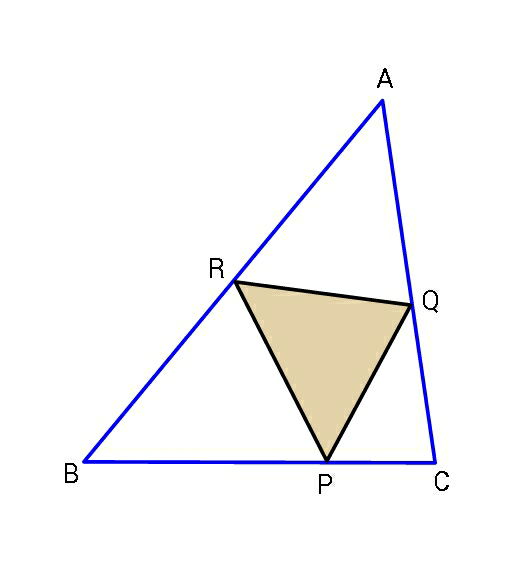
Commented by ajfour last updated on 09/Dec/19
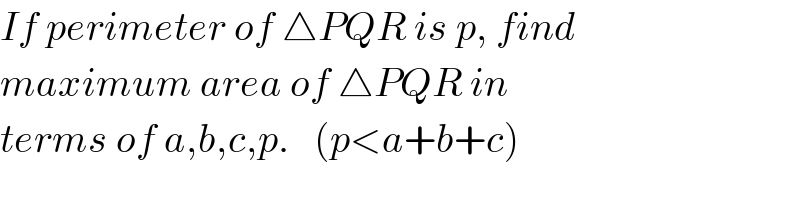
$${If}\:{perimeter}\:{of}\:\bigtriangleup{PQR}\:{is}\:{p},\:{find} \\ $$$${maximum}\:{area}\:{of}\:\bigtriangleup{PQR}\:{in} \\ $$$${terms}\:{of}\:{a},{b},{c},{p}.\:\:\:\left({p}<{a}+{b}+{c}\right)\: \\ $$
Commented by mr W last updated on 09/Dec/19
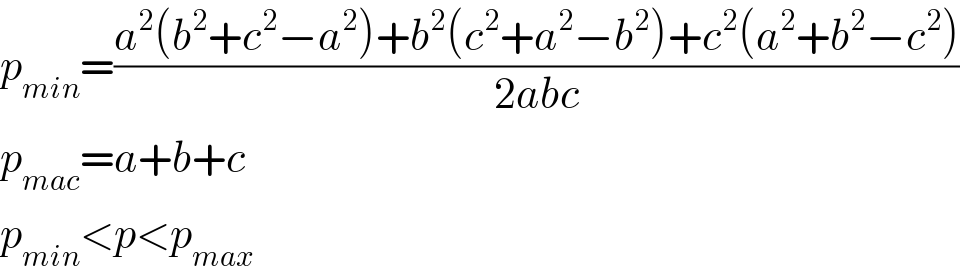
$${p}_{{min}} =\frac{{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)+{b}^{\mathrm{2}} \left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{\mathrm{2}{abc}} \\ $$$${p}_{{mac}} ={a}+{b}+{c} \\ $$$${p}_{{min}} <{p}<{p}_{{max}} \\ $$
Answered by mr W last updated on 10/Dec/19
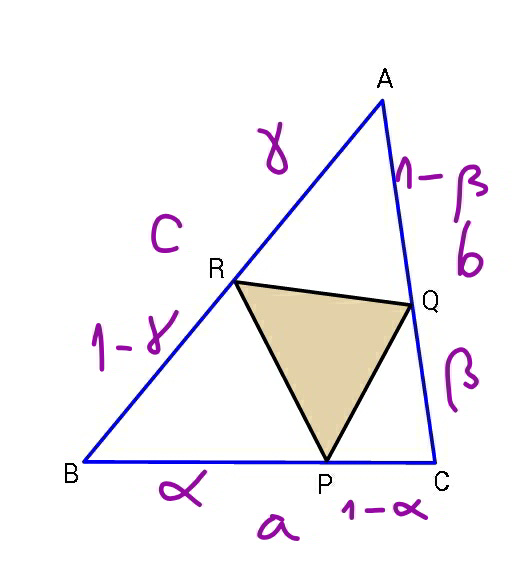
Commented by mr W last updated on 10/Dec/19
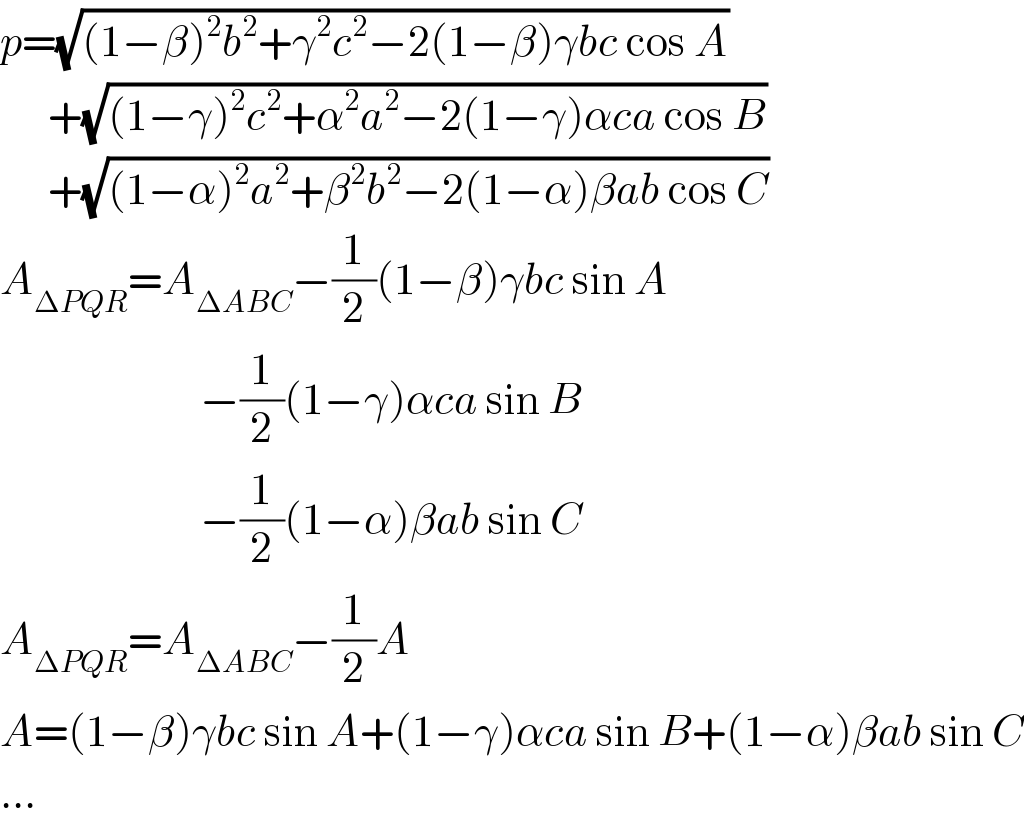
$${p}=\sqrt{\left(\mathrm{1}−\beta\right)^{\mathrm{2}} {b}^{\mathrm{2}} +\gamma^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\beta\right)\gamma{bc}\:\mathrm{cos}\:{A}} \\ $$$$\:\:\:\:\:\:+\sqrt{\left(\mathrm{1}−\gamma\right)^{\mathrm{2}} {c}^{\mathrm{2}} +\alpha^{\mathrm{2}} {a}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\gamma\right)\alpha{ca}\:\mathrm{cos}\:{B}} \\ $$$$\:\:\:\:\:\:+\sqrt{\left(\mathrm{1}−\alpha\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\beta^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\alpha\right)\beta{ab}\:\mathrm{cos}\:{C}} \\ $$$${A}_{\Delta{PQR}} ={A}_{\Delta{ABC}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\beta\right)\gamma{bc}\:\mathrm{sin}\:{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\gamma\right)\alpha{ca}\:\mathrm{sin}\:{B} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\alpha\right)\beta{ab}\:\mathrm{sin}\:{C} \\ $$$${A}_{\Delta{PQR}} ={A}_{\Delta{ABC}} −\frac{\mathrm{1}}{\mathrm{2}}{A} \\ $$$${A}=\left(\mathrm{1}−\beta\right)\gamma{bc}\:\mathrm{sin}\:{A}+\left(\mathrm{1}−\gamma\right)\alpha{ca}\:\mathrm{sin}\:{B}+\left(\mathrm{1}−\alpha\right)\beta{ab}\:\mathrm{sin}\:{C} \\ $$$$… \\ $$
