Question Number 75325 by TawaTawa last updated on 09/Dec/19

Answered by MJS last updated on 10/Dec/19
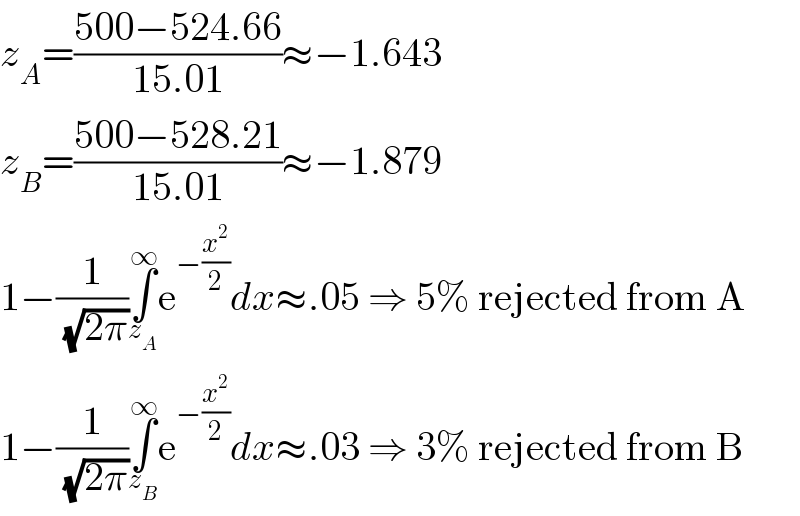
$${z}_{{A}} =\frac{\mathrm{500}−\mathrm{524}.\mathrm{66}}{\mathrm{15}.\mathrm{01}}\approx−\mathrm{1}.\mathrm{643} \\ $$$${z}_{{B}} =\frac{\mathrm{500}−\mathrm{528}.\mathrm{21}}{\mathrm{15}.\mathrm{01}}\approx−\mathrm{1}.\mathrm{879} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\underset{{z}_{{A}} } {\overset{\infty} {\int}}\mathrm{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx}\approx.\mathrm{05}\:\Rightarrow\:\mathrm{5\%}\:\mathrm{rejected}\:\mathrm{from}\:\mathrm{A} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\underset{{z}_{{B}} } {\overset{\infty} {\int}}\mathrm{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx}\approx.\mathrm{03}\:\Rightarrow\:\mathrm{3\%}\:\mathrm{rejected}\:\mathrm{from}\:\mathrm{B} \\ $$
Commented by TawaTawa last updated on 10/Dec/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate} \\ $$
