Question Number 75382 by Master last updated on 10/Dec/19
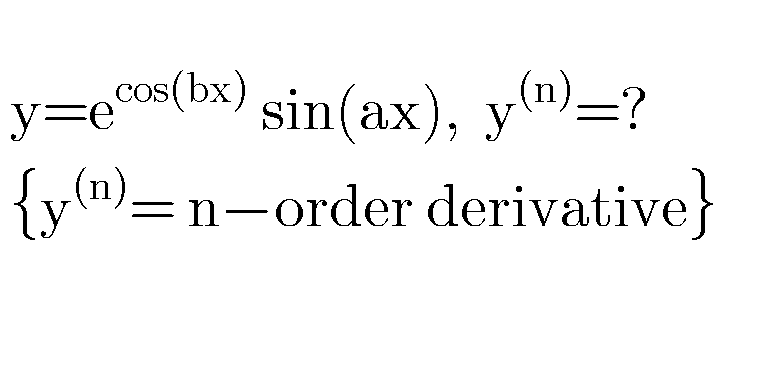
Commented by Master last updated on 10/Dec/19

$$\mathrm{please}\:\mathrm{solve} \\ $$
Answered by arkanmath7@gmail.com last updated on 10/Dec/19
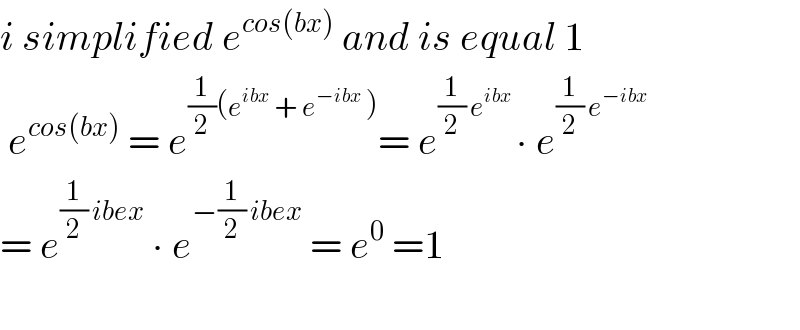
$${i}\:{simplified}\:{e}^{{cos}\left({bx}\right)} \:{and}\:{is}\:{equal}\:\mathrm{1} \\ $$$$\:{e}^{{cos}\left({bx}\right)} \:=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{ibx}} \:+\:{e}^{−{ibx}} \:\right)} =\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{{ibx}} \:} \centerdot\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−{ibx}} } \\ $$$$=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\:{ibex}} \:\centerdot\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}\:{ibex}} \:=\:{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$$$ \\ $$
Commented by Master last updated on 10/Dec/19
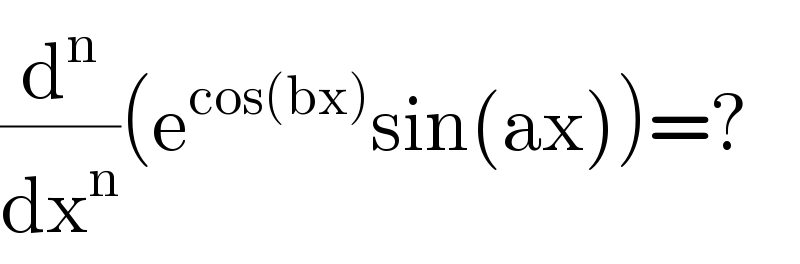
$$\frac{\mathrm{d}^{\mathrm{n}} }{\mathrm{dx}^{\mathrm{n}} }\left(\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \mathrm{sin}\left(\mathrm{ax}\right)\right)=? \\ $$
Commented by arkanmath7@gmail.com last updated on 10/Dec/19
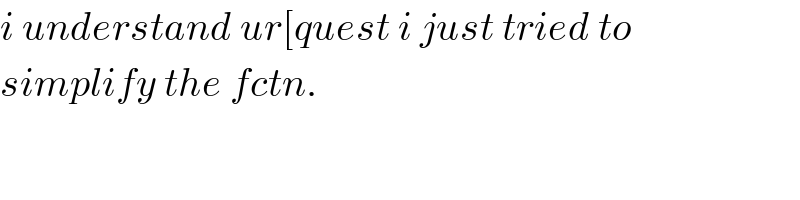
$${i}\:{understand}\:{ur}\left[{quest}\:{i}\:{just}\:{tried}\:{to}\right. \\ $$$${simplify}\:{the}\:{fctn}. \\ $$
Commented by MJS last updated on 10/Dec/19

$$\mathrm{e}^{\mathrm{cos}\:\left({bx}\right)} \neq\mathrm{1} \\ $$$$\mathrm{with}\:{x}=\mathrm{0} \\ $$$$\mathrm{e}^{\mathrm{cos}\:\left({bx}\right)} =\mathrm{e} \\ $$
