Menu Close

Question-75437

Tinku Tara 0 Comments
Pin




Question Number 75437 by Master last updated on 11/Dec/19
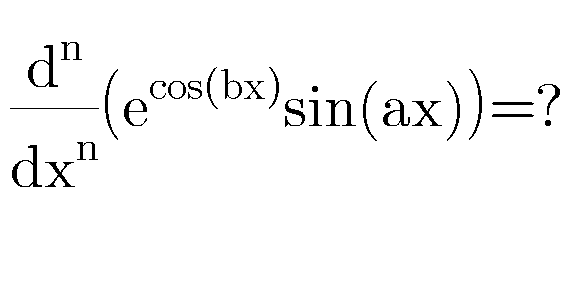
Commented by Master last updated on 11/Dec/19
sir mind is power please
$$\mathrm{sir}\:\boldsymbol{\mathrm{mind}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{power}}\:\:\mathrm{please}\: \\ $$
Commented by Master last updated on 11/Dec/19
sir mathmax
$$\mathrm{sir}\:\mathrm{mathmax} \\ $$
Commented by mathmax by abdo last updated on 12/Dec/19
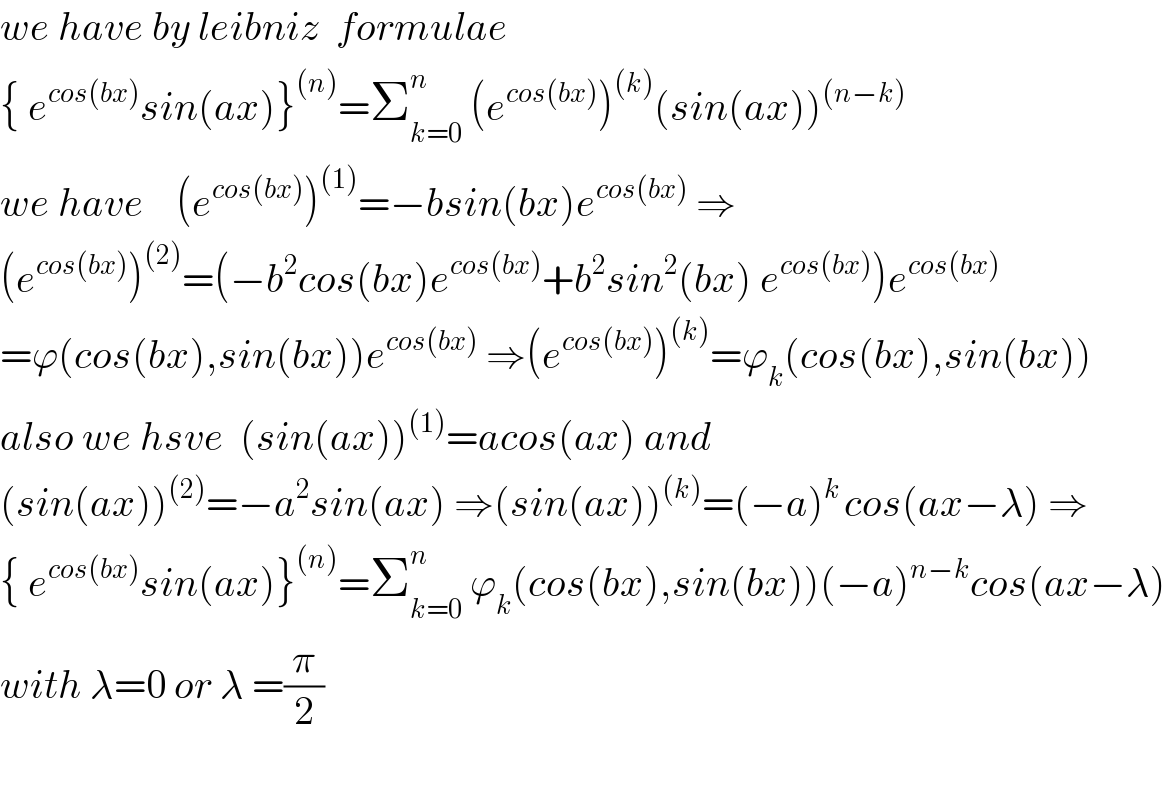
we have by leibniz formulae { e^(cos(bx)) sin(ax)}^((n)) =Σ_(k=0) ^n (e^(cos(bx)) )^((k)) (sin(ax))^((n−k)) we have (e^(cos(bx)) )^((1)) =−bsin(bx)e^(cos(bx)) ⇒ (e^(cos(bx)) )^((2)) =(−b^2 cos(bx)e^(cos(bx)) +b^2 sin^2 (bx) e^(cos(bx)) )e^(cos(bx)) =ϕ(cos(bx),sin(bx))e^(cos(bx)) ⇒(e^(cos(bx)) )^((k)) =ϕ_k (cos(bx),sin(bx)) also we hsve (sin(ax))^((1)) =acos(ax) and (sin(ax))^((2)) =−a^2 sin(ax) ⇒(sin(ax))^((k)) =(−a)^(k ) cos(ax−λ) ⇒ { e^(cos(bx)) sin(ax)}^((n)) =Σ_(k=0) ^n ϕ_k (cos(bx),sin(bx))(−a)^(n−k) cos(ax−λ) with λ=0 or λ =(π/2)
$${we}\:{have}\:{by}\:{leibniz}\:\:{formulae}\: \\ $$$$\left\{\:{e}^{{cos}\left({bx}\right)} {sin}\left({ax}\right)\right\}^{\left({n}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{{cos}\left({bx}\right)} \right)^{\left({k}\right)} \left({sin}\left({ax}\right)\right)^{\left({n}−{k}\right)} \\ $$$${we}\:{have}\:\:\:\:\left({e}^{{cos}\left({bx}\right)} \right)^{\left(\mathrm{1}\right)} =−{bsin}\left({bx}\right){e}^{{cos}\left({bx}\right)} \:\Rightarrow \\ $$$$\left({e}^{{cos}\left({bx}\right)} \right)^{\left(\mathrm{2}\right)} =\left(−{b}^{\mathrm{2}} {cos}\left({bx}\right){e}^{{cos}\left({bx}\right)} +{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \left({bx}\right)\:{e}^{{cos}\left({bx}\right)} \right){e}^{{cos}\left({bx}\right)} \\ $$$$=\varphi\left({cos}\left({bx}\right),{sin}\left({bx}\right)\right){e}^{{cos}\left({bx}\right)} \:\Rightarrow\left({e}^{{cos}\left({bx}\right)} \right)^{\left({k}\right)} =\varphi_{{k}} \left({cos}\left({bx}\right),{sin}\left({bx}\right)\right) \\ $$$${also}\:{we}\:{hsve}\:\:\left({sin}\left({ax}\right)\right)^{\left(\mathrm{1}\right)} ={acos}\left({ax}\right)\:{and}\: \\ $$$$\left({sin}\left({ax}\right)\right)^{\left(\mathrm{2}\right)} =−{a}^{\mathrm{2}} {sin}\left({ax}\right)\:\Rightarrow\left({sin}\left({ax}\right)\right)^{\left({k}\right)} =\left(−{a}\right)^{{k}\:} {cos}\left({ax}−\lambda\right)\:\Rightarrow \\ $$$$\left\{\:{e}^{{cos}\left({bx}\right)} {sin}\left({ax}\right)\right\}^{\left({n}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\varphi_{{k}} \left({cos}\left({bx}\right),{sin}\left({bx}\right)\right)\left(−{a}\right)^{{n}−{k}} {cos}\left({ax}−\lambda\right) \\ $$$${with}\:\lambda=\mathrm{0}\:{or}\:\lambda\:=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 12/Dec/19
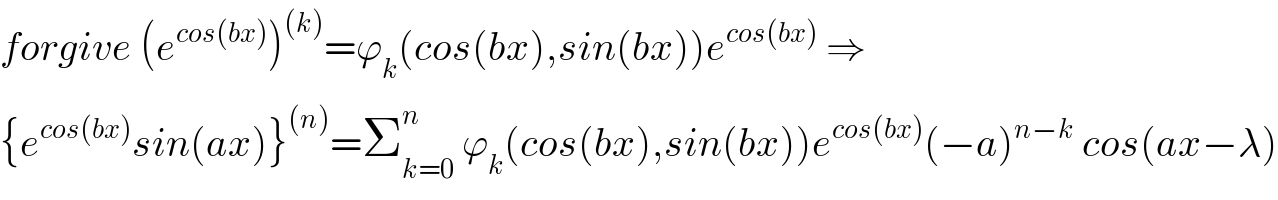
forgive (e^(cos(bx)) )^((k)) =ϕ_k (cos(bx),sin(bx))e^(cos(bx)) ⇒ {e^(cos(bx)) sin(ax)}^((n)) =Σ_(k=0) ^n ϕ_k (cos(bx),sin(bx))e^(cos(bx)) (−a)^(n−k) cos(ax−λ)
$${forgive}\:\left({e}^{{cos}\left({bx}\right)} \right)^{\left({k}\right)} =\varphi_{{k}} \left({cos}\left({bx}\right),{sin}\left({bx}\right)\right){e}^{{cos}\left({bx}\right)} \:\Rightarrow \\ $$$$\left\{{e}^{{cos}\left({bx}\right)} {sin}\left({ax}\right)\right\}^{\left({n}\right)} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\varphi_{{k}} \left({cos}\left({bx}\right),{sin}\left({bx}\right)\right){e}^{{cos}\left({bx}\right)} \left(−{a}\right)^{{n}−{k}} \:{cos}\left({ax}−\lambda\right) \\ $$
Commented by Master last updated on 12/Dec/19
thank you. great!
$$\mathrm{thank}\:\mathrm{you}.\:\mathrm{great}! \\ $$
Commented by mathmax by abdo last updated on 12/Dec/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by mind is power last updated on 12/Dec/19
hello sir sorry i have not times this days ,let f(x)=e^(cos(bx)) sin(ax) f′(x)={acos(ax)−bsin(bx)sin(ax)}e^(cos(bx)) lets find g_n (x) suche f^((n)) (x)=g_n (x)e^(cos(bx)) ⇒f^((n+1)) (x)=g_(n+1) (x)e^(cos(bx)) ={g′_n (x)−bsin(bx)g_n (x)}e^(cos(bx)) ⇒g_(n+1) (x)=g′_n (x)−bsin(bx)g_n (x) g_0 (x)=sin(ax) ⇒ { ((g_0 (x)=sin(ax))),((g_(n+1) (x)=g′_n (x)−bsin(bx)g_n (x))) :} f^n (x)=g_n (x)e^(cos(bx)) by reccursion
$$\mathrm{hello}\:\mathrm{sir}\:\mathrm{sorry}\:\:\mathrm{i}\:\mathrm{have}\:\:\mathrm{not}\:\mathrm{times}\:\mathrm{this}\:\mathrm{days}\:,\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \mathrm{sin}\left(\mathrm{ax}\right) \\ $$$$ \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\left\{\mathrm{acos}\left(\mathrm{ax}\right)−\mathrm{bsin}\left(\mathrm{bx}\right)\mathrm{sin}\left(\mathrm{ax}\right)\right\}\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \\ $$$$\mathrm{lets}\:\mathrm{find}\:\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right)\:\mathrm{suche} \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \\ $$$$\Rightarrow\mathrm{f}^{\left(\mathrm{n}+\mathrm{1}\right)} \left(\mathrm{x}\right)=\mathrm{g}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} =\left\{\mathrm{g}'_{\mathrm{n}} \left(\mathrm{x}\right)−\mathrm{bsin}\left(\mathrm{bx}\right)\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right)\right\}\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \\ $$$$\Rightarrow\mathrm{g}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{g}'_{\mathrm{n}} \left(\mathrm{x}\right)−\mathrm{bsin}\left(\mathrm{bx}\right)\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right) \\ $$$$\mathrm{g}_{\mathrm{0}} \left(\mathrm{x}\right)=\mathrm{sin}\left(\mathrm{ax}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{g}_{\mathrm{0}} \left(\mathrm{x}\right)=\mathrm{sin}\left(\mathrm{ax}\right)}\\{\mathrm{g}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{g}'_{\mathrm{n}} \left(\mathrm{x}\right)−\mathrm{bsin}\left(\mathrm{bx}\right)\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right)}\end{cases} \\ $$$$\mathrm{f}^{\mathrm{n}} \left(\mathrm{x}\right)=\mathrm{g}_{\mathrm{n}} \left(\mathrm{x}\right)\mathrm{e}^{\mathrm{cos}\left(\mathrm{bx}\right)} \:\:\:\:\mathrm{by}\:\mathrm{reccursion} \\ $$$$ \\ $$$$ \\ $$
Commented by Master last updated on 13/Dec/19
yes sir thank you.
$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *