Menu Close

Question-75440

Tinku Tara 0 Comments
Pin




Question Number 75440 by aliesam last updated on 11/Dec/19
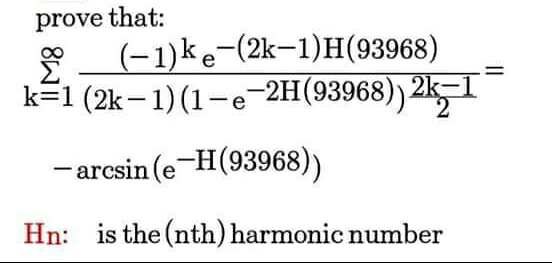
Commented by MJS last updated on 11/Dec/19
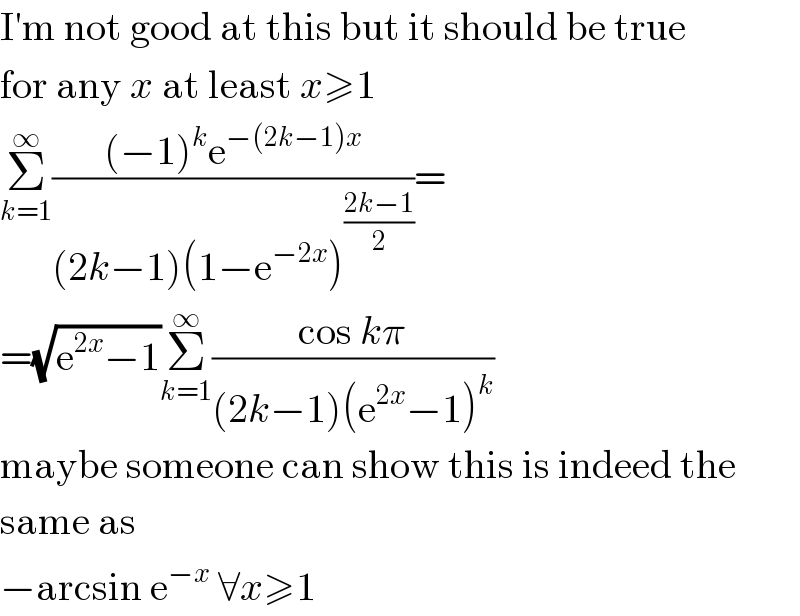
I′m not good at this but it should be true for any x at least x≥1 Σ_(k=1) ^∞ (((−1)^k e^(−(2k−1)x) )/((2k−1)(1−e^(−2x) )^((2k−1)/2) ))= =(√(e^(2x) −1))Σ_(k=1) ^∞ ((cos kπ)/((2k−1)(e^(2x) −1)^k )) maybe someone can show this is indeed the same as −arcsin e^(−x) ∀x≥1
$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{good}\:\mathrm{at}\:\mathrm{this}\:\mathrm{but}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{true} \\ $$$$\mathrm{for}\:\mathrm{any}\:{x}\:\mathrm{at}\:\mathrm{least}\:{x}\geqslant\mathrm{1} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} \mathrm{e}^{−\left(\mathrm{2}{k}−\mathrm{1}\right){x}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{e}^{−\mathrm{2}{x}} \right)^{\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}}} }= \\ $$$$=\sqrt{\mathrm{e}^{\mathrm{2}{x}} −\mathrm{1}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\:{k}\pi}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{2}{x}} −\mathrm{1}\right)^{{k}} } \\ $$$$\mathrm{maybe}\:\mathrm{someone}\:\mathrm{can}\:\mathrm{show}\:\mathrm{this}\:\mathrm{is}\:\mathrm{indeed}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{as} \\ $$$$−\mathrm{arcsin}\:\mathrm{e}^{−{x}} \:\forall{x}\geqslant\mathrm{1} \\ $$
Commented by mind is power last updated on 12/Dec/19
let α=H(93968) Σ_(k≥1) (((−1)^k e^(−(2k−1)α) )/((2k−1)(1−e^(−2α) )^((2k−1)/2) )) A=e^α (√(1−e^(−2α) ))Σ_(k≥1) (((−1)^k )/(2k−1))((e^(−2α) /(1−e^(−2α) )))^k Σ_(k≥1) (((−x)^k )/(2k−1)) arctan(x)=Σ_(k≥0) (((−1)^k x^(2k+1) )/(2k+1)) x=((e^(−2a) /(1−e^(−2a) )))^(1/2) A=e^a (√(1−e^(−2a) )).Σ_(k≥0) (((−1)^(k+1) )/(2k+1)).x^(2k+2) A=−.Σ_(k≥0) (((−1)^k x^(2k+1) )/(2k+1))=−arctan(x) x=(e^(−a) /( (√(1−e^(−2a) )))) lets show arctan((e^(−a) /( (√(1−e^(−2a) )))))=arcsin(e^(−a) ) mor generaly arctan((t/( (√(1−t^2 )))))=arcsin(t),0≤t<1 t=sin(α),α∈[0,(π/2)[ ⇒arctan(((sin(α))/( (√(1−sin^2 (α))))))=arctan(tg(α))=α=arcsin(sin(α)) ⇒arcsin(t)=arctan((t/( (√(1−t^2 ))))) since e^(−α) <1 ⇒arctan((e^(−a) /( (√(1−e^(−α) )))))=arcsin(e^(−α) ) ⇒A=−arcsin(e^(−α) )
$$\mathrm{let}\:\alpha=\mathrm{H}\left(\mathrm{93968}\right) \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{e}^{−\left(\mathrm{2k}−\mathrm{1}\right)\alpha} }{\left(\mathrm{2k}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{e}^{−\mathrm{2}\alpha} \right)^{\frac{\mathrm{2k}−\mathrm{1}}{\mathrm{2}}} } \\ $$$$\mathrm{A}=\mathrm{e}^{\alpha} \sqrt{\mathrm{1}−\mathrm{e}^{−\mathrm{2}\alpha} }\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}−\mathrm{1}}\left(\frac{\mathrm{e}^{−\mathrm{2}\alpha} }{\mathrm{1}−\mathrm{e}^{−\mathrm{2}\alpha} }\right)^{\mathrm{k}} \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{x}\right)^{\mathrm{k}} }{\mathrm{2k}−\mathrm{1}} \\ $$$$\mathrm{arctan}\left(\mathrm{x}\right)=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{2k}+\mathrm{1}} }{\mathrm{2k}+\mathrm{1}} \\ $$$$\mathrm{x}=\left(\frac{\mathrm{e}^{−\mathrm{2a}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{2a}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{A}=\mathrm{e}^{\mathrm{a}} \sqrt{\mathrm{1}−\mathrm{e}^{−\mathrm{2a}} }.\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }{\mathrm{2k}+\mathrm{1}}.\mathrm{x}^{\mathrm{2k}+\mathrm{2}} \\ $$$$\mathrm{A}=−.\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{2k}+\mathrm{1}} }{\mathrm{2k}+\mathrm{1}}=−\mathrm{arctan}\left(\mathrm{x}\right)\: \\ $$$$\mathrm{x}=\frac{\mathrm{e}^{−\mathrm{a}} }{\:\sqrt{\mathrm{1}−\mathrm{e}^{−\mathrm{2a}} }} \\ $$$$\mathrm{lets}\:\mathrm{show}\:\mathrm{arctan}\left(\frac{\mathrm{e}^{−\mathrm{a}} }{\:\sqrt{\mathrm{1}−\mathrm{e}^{−\mathrm{2a}} }}\right)=\mathrm{arcsin}\left(\mathrm{e}^{−\mathrm{a}} \right) \\ $$$$\mathrm{mor}\:\mathrm{generaly}\: \\ $$$$\mathrm{arctan}\left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\right)=\mathrm{arcsin}\left(\mathrm{t}\right),\mathrm{0}\leqslant\mathrm{t}<\mathrm{1} \\ $$$$\mathrm{t}=\mathrm{sin}\left(\alpha\right),\alpha\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\right.\right. \\ $$$$\Rightarrow\mathrm{arctan}\left(\frac{\mathrm{sin}\left(\alpha\right)}{\:\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \left(\alpha\right)}}\right)=\mathrm{arctan}\left(\mathrm{tg}\left(\alpha\right)\right)=\alpha=\mathrm{arcsin}\left(\mathrm{sin}\left(\alpha\right)\right) \\ $$$$\Rightarrow\mathrm{arcsin}\left(\mathrm{t}\right)=\mathrm{arctan}\left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{since}\:\mathrm{e}^{−\alpha} <\mathrm{1} \\ $$$$\Rightarrow\mathrm{arctan}\left(\frac{\mathrm{e}^{−\mathrm{a}} }{\:\sqrt{\mathrm{1}−\mathrm{e}^{−\alpha} }}\right)=\mathrm{arcsin}\left(\mathrm{e}^{−\alpha} \right) \\ $$$$\Rightarrow\mathrm{A}=−\mathrm{arcsin}\left(\mathrm{e}^{−\alpha} \right) \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 14/Dec/19
god bless you
$${god}\:{bless}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *