Question Number 75463 by indalecioneves last updated on 11/Dec/19

Answered by mr W last updated on 12/Dec/19
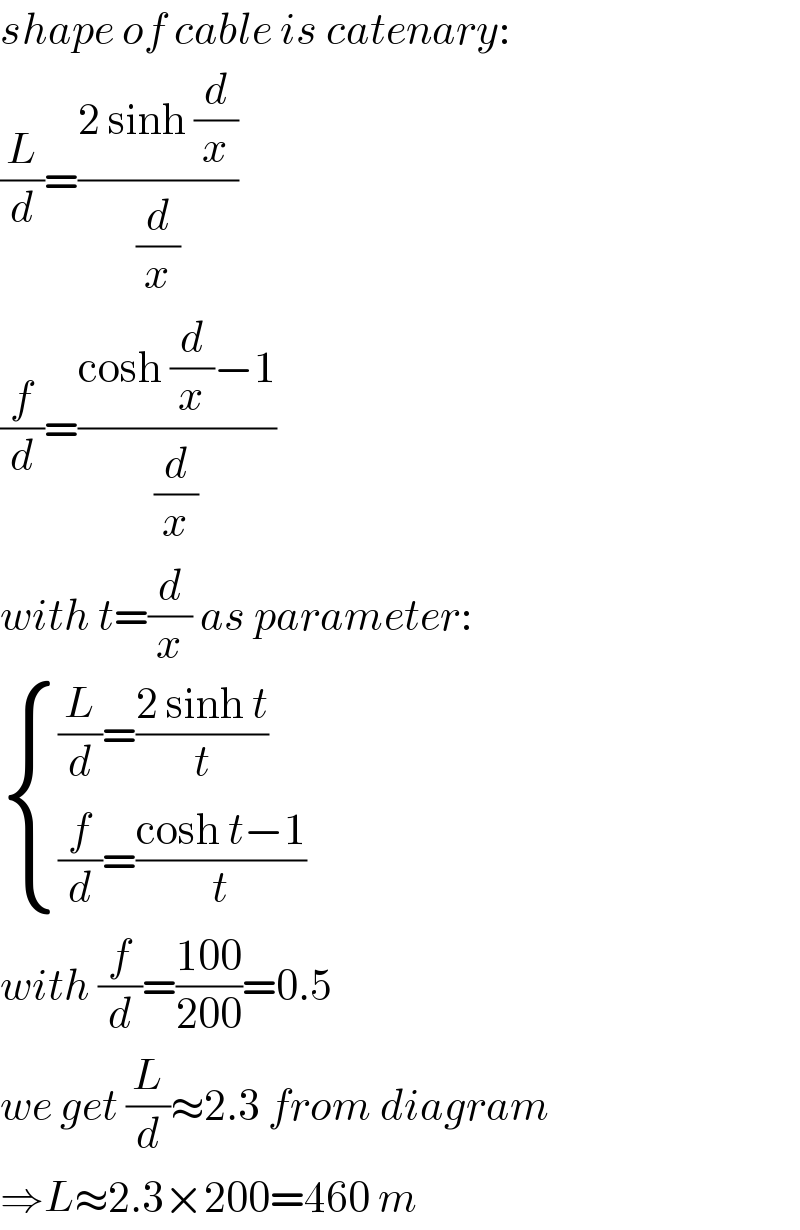
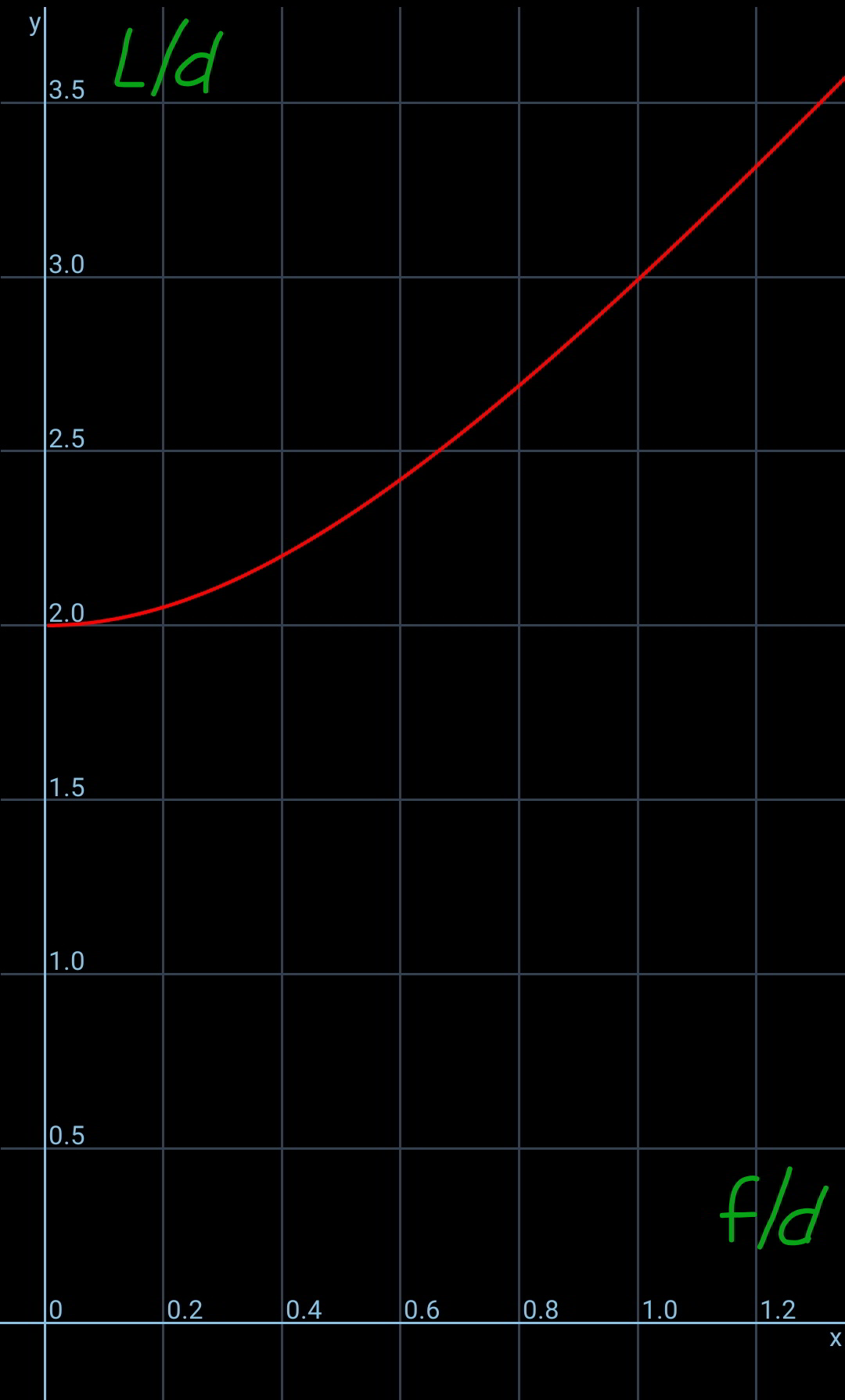
$${shape}\:{of}\:{cable}\:{is}\:{catenary}: \\ $$$$\frac{{L}}{{d}}=\frac{\mathrm{2}\:\mathrm{sinh}\:\frac{{d}}{{x}}}{\frac{{d}}{{x}}} \\ $$$$\frac{{f}}{{d}}=\frac{\mathrm{cosh}\:\frac{{d}}{{x}}−\mathrm{1}}{\frac{{d}}{{x}}} \\ $$$${with}\:{t}=\frac{{d}}{{x}}\:{as}\:{parameter}: \\ $$$$\begin{cases}{\frac{{L}}{{d}}=\frac{\mathrm{2}\:\mathrm{sinh}\:{t}}{{t}}}\\{\frac{{f}}{{d}}=\frac{\mathrm{cosh}\:{t}−\mathrm{1}}{{t}}}\end{cases} \\ $$$${with}\:\frac{{f}}{{d}}=\frac{\mathrm{100}}{\mathrm{200}}=\mathrm{0}.\mathrm{5} \\ $$$${we}\:{get}\:\frac{{L}}{{d}}\approx\mathrm{2}.\mathrm{3}\:{from}\:{diagram} \\ $$$$\Rightarrow{L}\approx\mathrm{2}.\mathrm{3}×\mathrm{200}=\mathrm{460}\:{m} \\ $$
Commented by mr W last updated on 11/Dec/19
Commented by indalecioneves last updated on 11/Dec/19

$${Thank}\:{you},\:{Sir}! \\ $$$${God}\:{bless}\:{you}! \\ $$
Answered by mr W last updated on 11/Dec/19
![Approximation as parabola: y=f((x/d))^2 y′=((2fx)/d^2 ) L=2∫_0 ^d (√(1+(((2fx)/d^2 ))^2 ))dx (L/d)=2∫_0 ^d (√(1+(((2fx)/d^2 ))^2 ))d((x/d)) (L/d)=2∫_0 ^1 (√(1+(((2fu)/d))^2 ))du (L/d)=(d/f)∫_0 ^1 (√(1+(((2fu)/d))^2 ))d(((2fu)/d)) ⇒(L/d)=(1/((2f)/d)){ln [((2f)/d)+(√(1+(((2f)/d))^2 ))]+((2f)/d)(√(1+(((2f)/d))^2 ))} with ((2f)/d)=((2×100)/(200))=1 ⇒(L/d)=ln (1+(√2))+(√2)=2.296 ⇒L=2.296×200≈460 m](https://www.tinkutara.com/question/Q75471.png)
$${Approximation}\:{as}\:{parabola}: \\ $$$${y}={f}\left(\frac{{x}}{{d}}\right)^{\mathrm{2}} \\ $$$${y}'=\frac{\mathrm{2}{fx}}{{d}^{\mathrm{2}} } \\ $$$${L}=\mathrm{2}\int_{\mathrm{0}} ^{{d}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{fx}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} }{dx} \\ $$$$\frac{{L}}{{d}}=\mathrm{2}\int_{\mathrm{0}} ^{{d}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{fx}}{{d}^{\mathrm{2}} }\right)^{\mathrm{2}} }{d}\left(\frac{{x}}{{d}}\right) \\ $$$$\frac{{L}}{{d}}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{fu}}{{d}}\right)^{\mathrm{2}} }{du} \\ $$$$\frac{{L}}{{d}}=\frac{{d}}{{f}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{fu}}{{d}}\right)^{\mathrm{2}} }{d}\left(\frac{\mathrm{2}{fu}}{{d}}\right) \\ $$$$\Rightarrow\frac{{L}}{{d}}=\frac{\mathrm{1}}{\frac{\mathrm{2}{f}}{{d}}}\left\{\mathrm{ln}\:\left[\frac{\mathrm{2}{f}}{{d}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{f}}{{d}}\right)^{\mathrm{2}} }\right]+\frac{\mathrm{2}{f}}{{d}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{f}}{{d}}\right)^{\mathrm{2}} }\right\} \\ $$$${with}\:\frac{\mathrm{2}{f}}{{d}}=\frac{\mathrm{2}×\mathrm{100}}{\mathrm{200}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{L}}{{d}}=\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\sqrt{\mathrm{2}}=\mathrm{2}.\mathrm{296} \\ $$$$\Rightarrow{L}=\mathrm{2}.\mathrm{296}×\mathrm{200}\approx\mathrm{460}\:{m} \\ $$
Commented by mr W last updated on 11/Dec/19

Commented by mr W last updated on 11/Dec/19
![we see the approximation as parabola is exact enough if the cable is flat. the advantage is that we can get L/d directly from f/d using the formula: (L/d)=(1/((2f)/d)){ln [((2f)/d)+(√(1+(((2f)/d))^2 ))]+((2f)/d)(√(1+(((2f)/d))^2 ))}](https://www.tinkutara.com/question/Q75473.png)
$${we}\:{see}\:{the}\:{approximation}\:{as} \\ $$$${parabola}\:{is}\:{exact}\:{enough}\:{if}\:{the} \\ $$$${cable}\:{is}\:{flat}. \\ $$$${the}\:{advantage}\:{is}\:{that}\:{we}\:{can}\:{get} \\ $$$${L}/{d}\:{directly}\:{from}\:{f}/{d}\:{using}\:{the} \\ $$$${formula}: \\ $$$$\frac{{L}}{{d}}=\frac{\mathrm{1}}{\frac{\mathrm{2}{f}}{{d}}}\left\{\mathrm{ln}\:\left[\frac{\mathrm{2}{f}}{{d}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{f}}{{d}}\right)^{\mathrm{2}} }\right]+\frac{\mathrm{2}{f}}{{d}}\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{f}}{{d}}\right)^{\mathrm{2}} }\right\} \\ $$
