Question Number 75505 by naka3546 last updated on 12/Dec/19
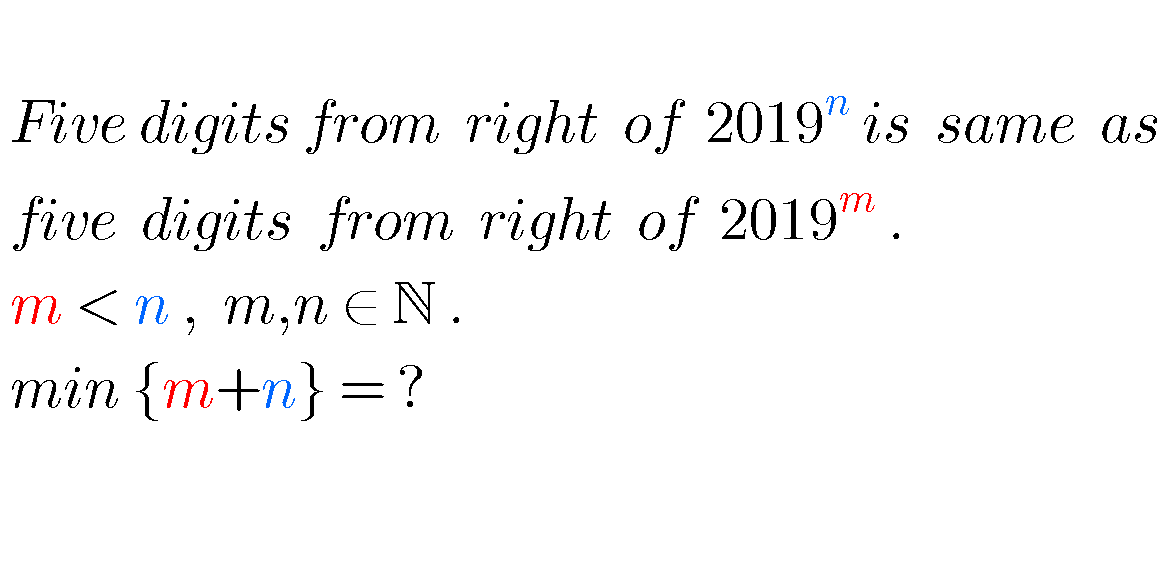
Commented by mr W last updated on 12/Dec/19

$${i}\:{don}'{t}\:{think}\:{such}\:{m}\:{and}\:{n}\:{exist}. \\ $$$${the}\:{last}\:{digit}\:{from}\:{right}\:{of}\:\mathrm{2019}^{{m}} \\ $$$${is}\:\mathrm{1}\:{or}\:\mathrm{9}.\:\mathrm{5}\:{times}\:{of}\:{it}\:{is}\:{always}\:\mathrm{5}, \\ $$$${but}\:{this}\:{can}\:{not}\:{be}\:\mathrm{2019}^{{n}} ,\:{since} \\ $$$${the}\:{last}\:{digit}\:{of}\:\mathrm{2019}^{{n}} \:{is}\:{also}\:\mathrm{1}\:{or}\:\mathrm{9}. \\ $$
Commented by MJS last updated on 12/Dec/19
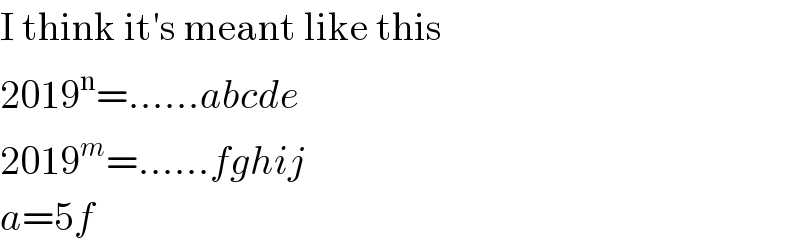
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{meant}\:\mathrm{like}\:\mathrm{this} \\ $$$$\mathrm{2019}^{\mathrm{n}} =……{abcde} \\ $$$$\mathrm{2019}^{{m}} =……{fghij} \\ $$$${a}=\mathrm{5}{f} \\ $$
Answered by MJS last updated on 12/Dec/19

$$\mathrm{2019}^{\mathrm{4}} =\mathrm{16}\:\mathrm{616}\:\mathrm{719}\:\mathrm{002}\:\mathrm{321} \\ $$$$\mathrm{2019}^{\mathrm{7}} =\mathrm{136}\:\mathrm{758}\:\mathrm{469}\:\mathrm{738}\:\mathrm{531}\:\mathrm{852}\:\mathrm{205}\:\mathrm{739} \\ $$$${m}=\mathrm{4}\wedge{n}=\mathrm{7} \\ $$$${m}+{n}=\mathrm{11} \\ $$
Commented by MJS last updated on 12/Dec/19
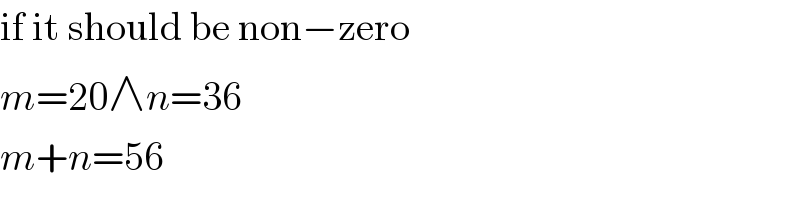
$$\mathrm{if}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{non}−\mathrm{zero} \\ $$$${m}=\mathrm{20}\wedge{n}=\mathrm{36} \\ $$$${m}+{n}=\mathrm{56} \\ $$
