Question Number 75512 by Master last updated on 12/Dec/19
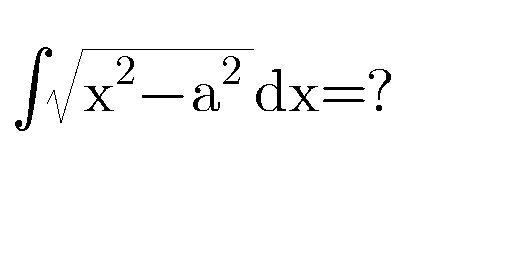
Commented by MJS last updated on 12/Dec/19

$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{standard}\:\mathrm{integral};\:\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:\mathrm{it}\:\mathrm{on} \\ $$$$\mathrm{any}\:\mathrm{table}\:\mathrm{of}\:\mathrm{integrals} \\ $$
Commented by JDamian last updated on 12/Dec/19

$${Tap}\:{on}\:\boldsymbol{\mathrm{Study}}\:>\:\boldsymbol{\mathrm{Integral}}\:\boldsymbol{\mathrm{Calculus}} \\ $$
Answered by Kunal12588 last updated on 12/Dec/19
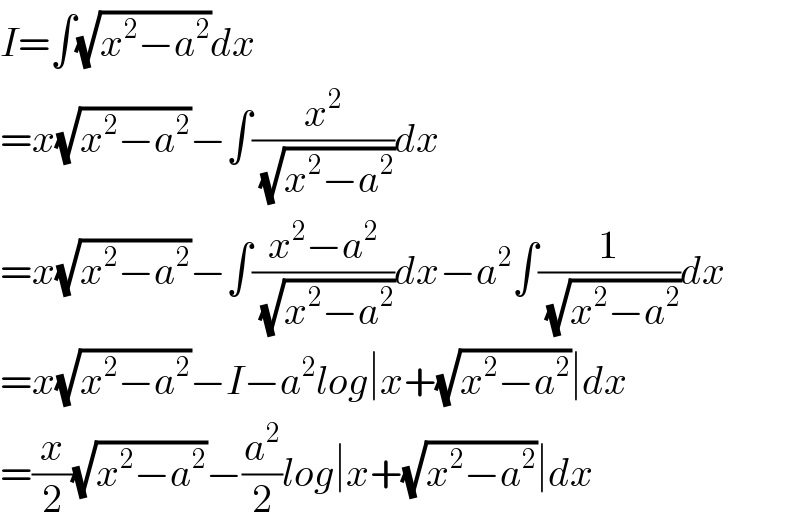
$${I}=\int\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx} \\ $$$$={x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{dx} \\ $$$$={x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\int\frac{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{dx}−{a}^{\mathrm{2}} \int\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{dx} \\ $$$$={x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−{I}−{a}^{\mathrm{2}} {log}\mid{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\mid{dx} \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{log}\mid{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\mid{dx} \\ $$
