Question Number 75552 by aliesam last updated on 12/Dec/19
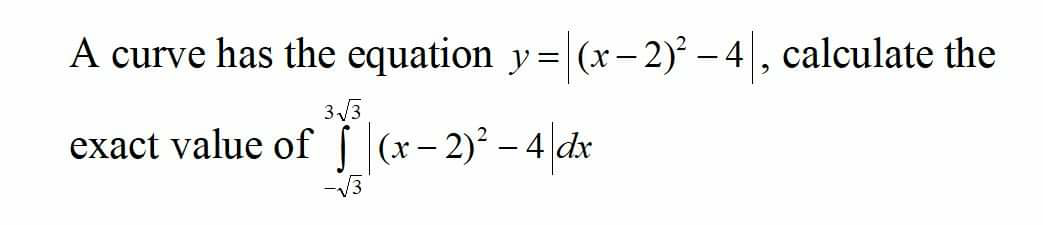
Commented by mathmax by abdo last updated on 12/Dec/19
![let I =∫_(−(√3)) ^(3(√3)) ∣(x−2)^2 −4∣dx ⇒I =∫_(−(√3)) ^(3(√3)) ∣x^2 −4x∣ dx =∫_(−(√3)) ^(3(√3)) ∣x∣∣x−4∣dx =∫_(−(√3)) ^0 (−x)(4−x)dx+∫_0 ^(3(√3)) x(x−4)dx =∫_(−(√3)) ^0 (x^2 −4x)dx +∫_0 ^(3(√3)) (x^2 −4x)dx =∫_(−(√3)) ^(3(√3)) (x^2 −4x)dx =[(x^3 /3)−2x^2 ]_(−(√3)) ^(3(√3)) =(((3(√3))^3 )/3)−2(3(√3))^2 −(((−(√3))^3 )/3) +2(−(√3))^2 =27(√3)−52 +(√3)+6 =28(√3)−46](https://www.tinkutara.com/question/Q75563.png)
$${let}\:{I}\:=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \:\mid\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\mid{dx}\:\:\Rightarrow{I}\:\:=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \mid{x}^{\mathrm{2}} −\mathrm{4}{x}\mid\:{dx} \\ $$$$=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \:\mid{x}\mid\mid{x}−\mathrm{4}\mid{dx}\:=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{0}} \left(−{x}\right)\left(\mathrm{4}−{x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{3}\sqrt{\mathrm{3}}} {x}\left({x}−\mathrm{4}\right){dx} \\ $$$$=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{0}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}\right){dx}\:+\int_{\mathrm{0}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}\right){dx} \\ $$$$=\int_{−\sqrt{\mathrm{3}}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}\right){dx}\:=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}^{\mathrm{2}} \right]_{−\sqrt{\mathrm{3}}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \:=\frac{\left(\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}\left(\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$−\frac{\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }{\mathrm{3}}\:+\mathrm{2}\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{27}\sqrt{\mathrm{3}}−\mathrm{52}\:+\sqrt{\mathrm{3}}+\mathrm{6}\:=\mathrm{28}\sqrt{\mathrm{3}}−\mathrm{46} \\ $$
Answered by Kunal12588 last updated on 12/Dec/19
![I=∫_(−(√3)) ^( 3(√3)) ∣(x−2)^2 −4∣dx =∫_(−(√3)) ^( 0) [(x−2)^2 −4]dx−∫_0 ^( 4) [(x−2)^2 −4]dx +∫_4 ^(3(√3)) [(x−2)^2 −4]dx =[(1/3)(x−2)^3 −4(x−2)]_(−(√3)) ^0 −[(1/3)(x−2)^3 −4(x−2)]_0 ^4 +[(1/3)(x−2)^3 −4(x−2)]_4 ^(3(√3)) =[(8/3)+8+(1/3)(2+(√3))^3 −(2+(√3))]−[(8/3)−8−(8/3)+8]+[(1/3)(3(√3)−2)^3 −4(3(√3)−2)−(8/3)+8] pls calculate](https://www.tinkutara.com/question/Q75554.png)
$${I}=\int_{−\sqrt{\mathrm{3}}} ^{\:\mathrm{3}\sqrt{\mathrm{3}}} \mid\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\mid{dx} \\ $$$$=\int_{−\sqrt{\mathrm{3}}} ^{\:\mathrm{0}} \left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\right]{dx}−\int_{\mathrm{0}} ^{\:\mathrm{4}} \left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\right]{dx} \\ $$$$\:\:\:\:\:\:\:\:\:+\int_{\mathrm{4}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \left[\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\right]{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{4}\left({x}−\mathrm{2}\right)\right]_{−\sqrt{\mathrm{3}}} ^{\mathrm{0}} −\left[\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{4}\left({x}−\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:+\left[\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{4}\left({x}−\mathrm{2}\right)\right]_{\mathrm{4}} ^{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$=\left[\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{8}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{3}} −\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right]−\left[\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{8}−\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{8}\right]+\left[\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{4}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{2}\right)−\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{8}\right] \\ $$$${pls}\:{calculate} \\ $$
