Question Number 75570 by naka3546 last updated on 12/Dec/19
Commented by naka3546 last updated on 12/Dec/19
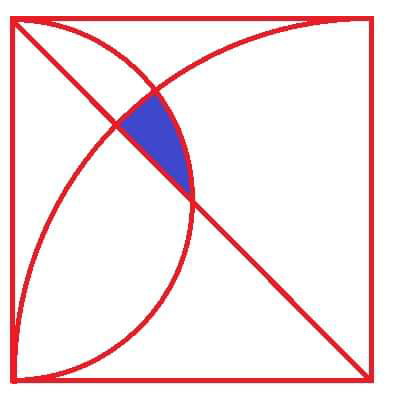
![(([ blue area ])/([ square area ])) = ?](https://www.tinkutara.com/question/Q75571.png)
$$\frac{\left[\:{blue}\:\:{area}\:\right]}{\left[\:{square}\:\:{area}\:\right]}\:\:=\:\:? \\ $$
Answered by mr W last updated on 13/Dec/19
Commented by mr W last updated on 13/Dec/19
![METHOD 1 say side length of square = 2 (2−r cos θ)^2 +(r sin θ−1)^2 =1^2 r^2 −2(sin θ+2 cos θ)r+4=0 sin θ+2 cos θ=(√5) cos (θ−α) with α=tan^(−1) (1/2) r^2 −2(√5) cos (θ−α)r+4=0 ⇒r=(√5) cos (θ−α)−(√(5 cos^2 (θ−α)−4)) r^2 =10 cos^2 (θ−α)−2(√5) cos (θ−α)(√(5 cos^2 (θ−α)−4))−4 2^2 −2(√5) cos (θ_1 −α)2+4=0 ⇒cos (θ_1 −α)=(2/( (√5)))=cos α ⇒θ_1 =2α=2 tan^(−1) (1/2) A_(blue) =∫_(π/4) ^θ_1 (1/2)(2^2 −r^2 )dθ =(1/2)∫_(π/4) ^(2α) (8−10 cos^2 (θ−α)+2(√5) cos (θ−α)(√(5 cos^2 (θ−α)−4)))dθ =∫_(π/4) ^(2α) (4−5 cos^2 (θ−α)+(√5) cos (θ−α)(√(5 cos^2 (θ−α)−4)))d(θ−α) =∫_((π/4)−α) ^α (4−5 cos^2 ϕ+(√5) cos ϕ(√(5 cos^2 ϕ−4)))dϕ =∫_((π/4)−α) ^α ((3/2)−(5/2) cos 2ϕ+(√5) cos ϕ(√(1−5 sin^2 ϕ)))dϕ =[(3/2)ϕ−(5/4)sin 2ϕ]_((π/4)−α) ^α +∫_((π/4)−α) ^α (√(1−((√5) sin ϕ)^2 )) d((√5) sin ϕ) =[(3/2)ϕ−(5/4)sin 2ϕ+(1/2)sin^(−1) ((√5) sin ϕ)+(((√5) sin ϕ (√(1−5 sin^2 ϕ)))/2)]_((π/4)−α) ^α =(1/2)[3(2 tan^(−1) (1/2)−(π/4))−(5/2)((4/5)−(3/5))+(π/2)−(π/4)+0−(1/2)] =3 tan^(−1) (1/2)−((π+2)/4) A_(square) =2^2 =4 (A_(blue) /A_(square) )=(3/4) tan^(−1) (1/2)−((π+2)/(16))≈0.026386](https://www.tinkutara.com/question/Q75579.png)
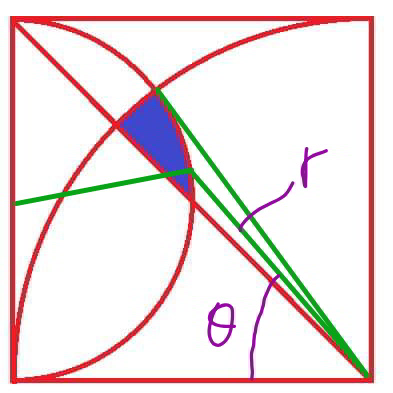
$${METHOD}\:\mathrm{1} \\ $$$${say}\:{side}\:{length}\:{of}\:{square}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{2}−{r}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({r}\:\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{sin}\:\theta+\mathrm{2}\:\mathrm{cos}\:\theta\right){r}+\mathrm{4}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{sin}\:\theta+\mathrm{2}\:\mathrm{cos}\:\theta=\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right) \\ $$$${with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right){r}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{r}=\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right)−\sqrt{\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)−\mathrm{4}} \\ $$$${r}^{\mathrm{2}} =\mathrm{10}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)−\mathrm{2}\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right)\sqrt{\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)−\mathrm{4}}−\mathrm{4} \\ $$$$ \\ $$$$\mathrm{2}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta_{\mathrm{1}} −\alpha\right)\mathrm{2}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\theta_{\mathrm{1}} −\alpha\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}=\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\theta_{\mathrm{1}} =\mathrm{2}\alpha=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${A}_{{blue}} =\int_{\frac{\pi}{\mathrm{4}}} ^{\theta_{\mathrm{1}} } \frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{\mathrm{2}} −{r}^{\mathrm{2}} \right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{2}\alpha} \left(\mathrm{8}−\mathrm{10}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)+\mathrm{2}\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right)\sqrt{\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)−\mathrm{4}}\right){d}\theta \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{2}\alpha} \left(\mathrm{4}−\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)+\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\alpha\right)\sqrt{\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\alpha\right)−\mathrm{4}}\right){d}\left(\theta−\alpha\right) \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}−\alpha} ^{\alpha} \left(\mathrm{4}−\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\varphi+\sqrt{\mathrm{5}}\:\mathrm{cos}\:\varphi\sqrt{\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:\varphi−\mathrm{4}}\right){d}\varphi \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}−\alpha} ^{\alpha} \left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2}\varphi+\sqrt{\mathrm{5}}\:\mathrm{cos}\:\varphi\sqrt{\mathrm{1}−\mathrm{5}\:\mathrm{sin}^{\mathrm{2}} \:\varphi}\right){d}\varphi \\ $$$$=\left[\frac{\mathrm{3}}{\mathrm{2}}\varphi−\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}\varphi\right]_{\frac{\pi}{\mathrm{4}}−\alpha} ^{\alpha} +\int_{\frac{\pi}{\mathrm{4}}−\alpha} ^{\alpha} \sqrt{\mathrm{1}−\left(\sqrt{\mathrm{5}}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} }\:{d}\left(\sqrt{\mathrm{5}}\:\mathrm{sin}\:\varphi\right) \\ $$$$=\left[\frac{\mathrm{3}}{\mathrm{2}}\varphi−\frac{\mathrm{5}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}\varphi+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{5}}\:\mathrm{sin}\:\varphi\right)+\frac{\sqrt{\mathrm{5}}\:\mathrm{sin}\:\varphi\:\sqrt{\mathrm{1}−\mathrm{5}\:\mathrm{sin}^{\mathrm{2}} \:\varphi}}{\mathrm{2}}\right]_{\frac{\pi}{\mathrm{4}}−\alpha} ^{\alpha} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{3}\left(\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{5}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{3}}{\mathrm{5}}\right)+\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}+\mathrm{0}−\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$=\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi+\mathrm{2}}{\mathrm{4}} \\ $$$${A}_{{square}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\frac{{A}_{{blue}} }{{A}_{{square}} }=\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi+\mathrm{2}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{026386} \\ $$
Answered by mr W last updated on 13/Dec/19
Commented by mr W last updated on 13/Dec/19
$${thanks}\:{for}\:{encouraging},\:{sir}! \\ $$
Commented by mr W last updated on 13/Dec/19

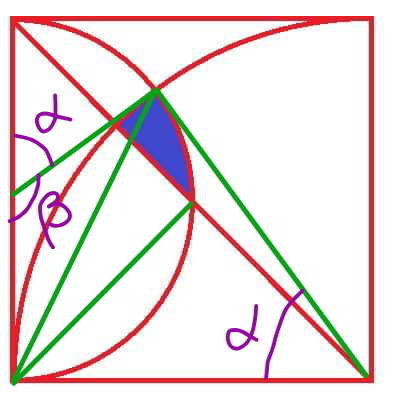
$${METHOD}\:\mathrm{2} \\ $$$${say}\:{square}\:{side}\:{length}\:=\mathrm{2} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\mathrm{1}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\mathrm{1}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right)=\mathrm{1}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{blue}} =\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right)+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\beta−\mathrm{sin}\:\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:−\frac{\pi×\mathrm{2}^{\mathrm{2}} }{\mathrm{8}}+\frac{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\right) \\ $$$${A}_{{blue}} =\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right)+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right)−\frac{\pi}{\mathrm{2}}+\mathrm{1}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{blue}} =\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{8}}{\mathrm{5}}+\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{5}}−\frac{\pi}{\mathrm{2}}+\mathrm{1}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{blue}} =\mathrm{3}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi+\mathrm{2}}{\mathrm{4}} \\ $$$${A}_{{square}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\frac{{A}_{{blue}} }{{A}_{{square}} }=\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi+\mathrm{2}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{026386} \\ $$
Commented by behi83417@gmail.com last updated on 13/Dec/19

$$\mathrm{sir}\:\mathrm{mrW}!\:\mathrm{you}\:\mathrm{are}\:\mathrm{amazing}! \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{being}\:\mathrm{at}\:\mathrm{this}\:\mathrm{forum}. \\ $$
