Question-75618

Question Number 75618 by peter frank last updated on 13/Dec/19

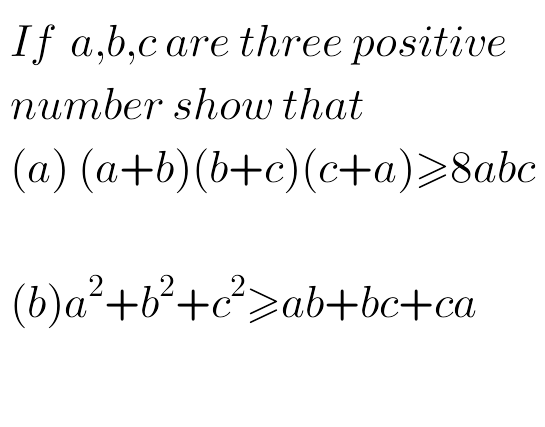
Commented by mind is power last updated on 13/Dec/19

use x+y≥2(√(xy)) (a+b)≥2(√(ab)),(a+c)≥2(√(ac)),c+a≥2(√(ca)) ⇒(a+b)(b+c)(c+a)≥2(√(ab)).2(√(bc)).2(√(ac))=8abc (b) by cauchy shwartz Σx_i .y_i ≤(√((Σx_i ^2 ))).(√(Σy_i ^2 )) x=(a,b,c) y=(b,c,a⇒ ab+bc+ca≤(√((a^2 +b^2 +c^2 ))).(√((b^2 +c^2 +a^2 )))=(a^2 +b^2 +c^2 ) 2nd methode (a+b)(b+c)(c+a) =2abc+a^2 b+a^2 c+b^2 a+b^2 c+c^2 a+c^2 b we use AM−GM inequality ⇒((a^2 b+a^2 c+ab^2 +ac^2 +b^2 c+c^2 b)/6)≥(a^2 b.a^2 c.b^2 a.b^2 c.c^2 a.c^2 b)^(1/6) =(a^6 b^6 c^6 )^(1/6) ⇒a^2 b+a^2 c+b^2 c+b^2 a+c^2 a+c^2 b≥6(abc) ⇒(a+b)(a+c)(b+c)≥2abc+6abc=8abc 2)a^2 +b^2 +c^2 =(1/2)(a^2 +b^2 )+(1/2)(a^2 +c^2 )+(1/2)(b^2 +c^2 )≥(1/2)2ab+(1/2).2ac+(1/2).2bc=ab+bc+ac

$$\mathrm{use}\:\mathrm{x}+\mathrm{y}\geqslant\mathrm{2}\sqrt{\mathrm{xy}} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)\geqslant\mathrm{2}\sqrt{\mathrm{ab}},\left(\mathrm{a}+\mathrm{c}\right)\geqslant\mathrm{2}\sqrt{\mathrm{ac}},\mathrm{c}+\mathrm{a}\geqslant\mathrm{2}\sqrt{\mathrm{ca}} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{c}+\mathrm{a}\right)\geqslant\mathrm{2}\sqrt{\mathrm{ab}}.\mathrm{2}\sqrt{\mathrm{bc}}.\mathrm{2}\sqrt{\mathrm{ac}}=\mathrm{8abc} \\ $$$$\left(\mathrm{b}\right) \\ $$$$\mathrm{by}\:\mathrm{cauchy}\:\mathrm{shwartz}\: \\ $$$$\Sigma\mathrm{x}_{\mathrm{i}} .\mathrm{y}_{\mathrm{i}} \leqslant\sqrt{\left(\Sigma\mathrm{x}_{\mathrm{i}} ^{\mathrm{2}} \right)}.\sqrt{\Sigma\mathrm{y}_{\mathrm{i}} ^{\mathrm{2}} } \\ $$$$\mathrm{x}=\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\:\mathrm{y}=\left(\mathrm{b},\mathrm{c},\mathrm{a}\Rightarrow\right. \\ $$$$\left.\mathrm{a}\left.\mathrm{b}+\mathrm{bc}+\mathrm{ca}\leqslant\sqrt{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right.}\right).\sqrt{\left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right.}\right)=\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right) \\ $$$$\mathrm{2nd}\:\mathrm{methode} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{c}+\mathrm{a}\right) \\ $$$$=\mathrm{2abc}+\mathrm{a}^{\mathrm{2}} \mathrm{b}+\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{b}^{\mathrm{2}} \mathrm{a}+\mathrm{b}^{\mathrm{2}} \mathrm{c}+\mathrm{c}^{\mathrm{2}} \mathrm{a}+\mathrm{c}^{\mathrm{2}} \mathrm{b} \\ $$$$\mathrm{we}\:\mathrm{use}\:\mathrm{AM}−\mathrm{GM}\:\mathrm{inequality} \\ $$$$\Rightarrow\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}+\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{ab}^{\mathrm{2}} +\mathrm{ac}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}+\mathrm{c}^{\mathrm{2}} \mathrm{b}}{\mathrm{6}}\geqslant\left(\mathrm{a}^{\mathrm{2}} \mathrm{b}.\mathrm{a}^{\mathrm{2}} \mathrm{c}.\mathrm{b}^{\mathrm{2}} \mathrm{a}.\mathrm{b}^{\mathrm{2}} \mathrm{c}.\mathrm{c}^{\mathrm{2}} \mathrm{a}.\mathrm{c}^{\mathrm{2}} \mathrm{b}\right)^{\frac{\mathrm{1}}{\mathrm{6}}} =\left(\mathrm{a}^{\mathrm{6}} \mathrm{b}^{\mathrm{6}} \mathrm{c}^{\mathrm{6}} \right)^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} \mathrm{b}+\mathrm{a}^{\mathrm{2}} \mathrm{c}+\mathrm{b}^{\mathrm{2}} \mathrm{c}+\mathrm{b}^{\mathrm{2}} \mathrm{a}+\mathrm{c}^{\mathrm{2}} \mathrm{a}+\mathrm{c}^{\mathrm{2}} \mathrm{b}\geqslant\mathrm{6}\left(\mathrm{abc}\right) \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}+\mathrm{c}\right)\left(\mathrm{b}+\mathrm{c}\right)\geqslant\mathrm{2abc}+\mathrm{6abc}=\mathrm{8abc} \\ $$$$\left.\mathrm{2}\right)\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)\geqslant\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2ab}+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2ac}+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2bc}=\mathrm{ab}+\mathrm{bc}+\mathrm{ac} \\ $$

Commented by peter frank last updated on 14/Dec/19

$${thank}\:{you}\:{very}\:{much} \\ $$

Commented by mind is power last updated on 14/Dec/19

$$\mathrm{withe}\:\mathrm{Pleasur} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply