Question Number 75627 by liki last updated on 14/Dec/19
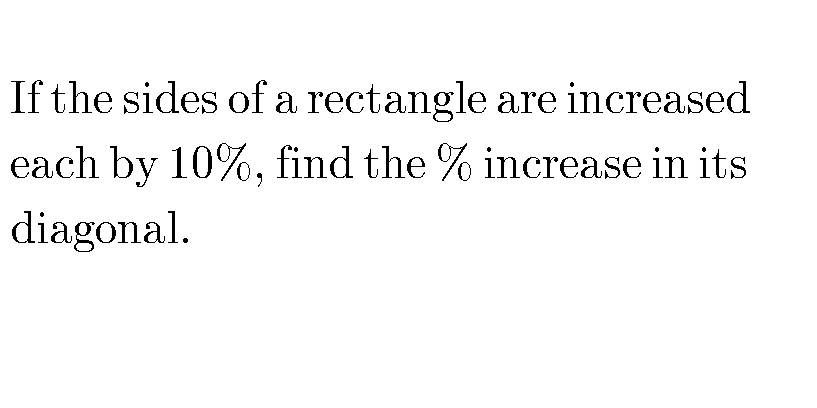
Answered by $@ty@m123 last updated on 14/Dec/19

$$\boldsymbol{{Initially}}, \\ $$$${Length}={l} \\ $$$${Breadth}={b} \\ $$$$\therefore\:{Diagonal}\:\:\:\boldsymbol{{d}}=\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:……\left(\mathrm{1}\right) \\ $$$$\boldsymbol{{After}}\:\boldsymbol{{inceasing}}\:\boldsymbol{{sides}}\:\boldsymbol{{by}}\:\mathrm{10\%}, \\ $$$${Length}={l}\left(\mathrm{1}+\frac{\mathrm{10}}{\mathrm{100}}\right)=\frac{\mathrm{110}}{\mathrm{100}}{l}=\frac{\mathrm{11}}{\mathrm{10}}{l} \\ $$$${Breadth}={b}\left(\mathrm{1}+\frac{\mathrm{10}}{\mathrm{100}}\right)=\frac{\mathrm{110}}{\mathrm{100}}{b}=\frac{\mathrm{11}}{\mathrm{10}}{b} \\ $$$$\therefore\:{Diagonal}\:\:\:\:\boldsymbol{{D}}=\sqrt{\left(\frac{\mathrm{11}}{\mathrm{10}}{l}\right)^{\mathrm{2}} +\left(\frac{\mathrm{11}}{\mathrm{10}}{b}\right)^{\mathrm{2}} } \\ $$$$\:\Rightarrow\:\:\boldsymbol{{D}}=\frac{\mathrm{11}}{\mathrm{10}}\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:…….\left(\mathrm{2}\right) \\ $$$$\therefore\:\boldsymbol{{Percentage}}\:\boldsymbol{{increase}}\:\boldsymbol{{in}}\:\boldsymbol{{diagonal}}\: \\ $$$$=\frac{{D}−{d}}{{d}}×\mathrm{100} \\ $$$$=\frac{\left(\frac{\mathrm{11}}{\mathrm{10}}\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:−\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}{\:\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }}×\mathrm{100} \\ $$$$=\frac{\left.\left(\frac{\mathrm{11}}{\mathrm{10}}\:−\mathrm{1}\right)\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}{\:\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }}×\mathrm{100} \\ $$$$=\frac{\mathrm{11}−\mathrm{10}}{\mathrm{10}}×\mathrm{100} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}×\mathrm{100} \\ $$$$=\mathrm{10\%} \\ $$
Commented by liki last updated on 14/Dec/19

$$….\boldsymbol{{Thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}}\:\boldsymbol{{be}}\:\boldsymbol{{blessed}} \\ $$
