Question Number 75641 by aliesam last updated on 14/Dec/19
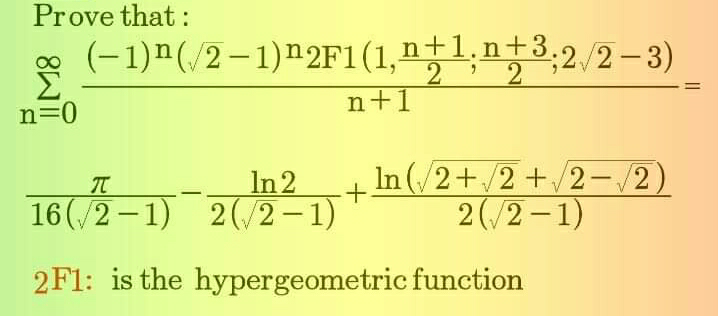
Commented by vishalbhardwaj last updated on 15/Dec/19
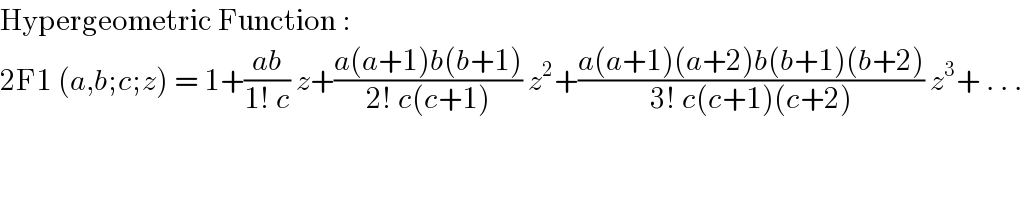
$$\mathrm{Hypergeometric}\:\mathrm{Function}\::\: \\ $$$$\mathrm{2F1}\:\left({a},{b};{c};{z}\right)\:=\:\mathrm{1}+\frac{{ab}}{\mathrm{1}!\:{c}}\:{z}+\frac{{a}\left({a}+\mathrm{1}\right){b}\left({b}+\mathrm{1}\right)}{\mathrm{2}!\:{c}\left({c}+\mathrm{1}\right)}\:{z}^{\mathrm{2}} +\frac{{a}\left({a}+\mathrm{1}\right)\left({a}+\mathrm{2}\right){b}\left({b}+\mathrm{1}\right)\left({b}+\mathrm{2}\right)}{\mathrm{3}!\:{c}\left({c}+\mathrm{1}\right)\left({c}+\mathrm{2}\right)}\:{z}^{\mathrm{3}} +\:.\:.\:. \\ $$
Answered by vishalbhardwaj last updated on 15/Dec/19
![Σ_(n=0) ^∞ (((−1)^n ((√2)−1)^n [1+((1.(((n+1))/2))/(1! (((n+3))/2))) (2(√2)−3)+((1.2(((n+1)(n+3))/(2.2)))/(2! (((n+3)(n+5))/(2.2)))) (2(√2)−3)^2 +((1.2.3 (((n+1)(n+3)(n+5))/(2.2.2)))/(3! (((n+3)(n+5)(n+7))/(2.2.2)))) (2(√2)−3)^3 +...])/(n+1)) =Σ_(n=0) ^∞ (((−1)^n ((√2)−1)^n [1+(((n+1))/((n+3)))(2(√2)−3)+(((n+1))/((n+5))) (2(√2)−3)^2 +(((n+1))/((n+7))) (2(√2)−3)^3 +...])/(n+1)) solve it](https://www.tinkutara.com/question/Q75652.png)
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} \left[\mathrm{1}+\frac{\mathrm{1}.\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}}{\mathrm{1}!\:\frac{\left(\mathrm{n}+\mathrm{3}\right)}{\mathrm{2}}}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)+\frac{\mathrm{1}.\mathrm{2}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{3}\right)}{\mathrm{2}.\mathrm{2}}}{\mathrm{2}!\:\frac{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{5}\right)}{\mathrm{2}.\mathrm{2}}}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{2}} +\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}\:\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{5}\right)}{\mathrm{2}.\mathrm{2}.\mathrm{2}}}{\mathrm{3}!\:\frac{\left(\mathrm{n}+\mathrm{3}\right)\left(\mathrm{n}+\mathrm{5}\right)\left(\mathrm{n}+\mathrm{7}\right)}{\mathrm{2}.\mathrm{2}.\mathrm{2}}}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{3}} +…\right]}{\mathrm{n}+\mathrm{1}} \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} \left[\mathrm{1}+\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{n}+\mathrm{3}\right)}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)+\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{n}+\mathrm{5}\right)}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{2}} +\frac{\left(\mathrm{n}+\mathrm{1}\right)}{\left(\mathrm{n}+\mathrm{7}\right)}\:\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{3}} +…\right]}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{solve}\:\mathrm{it} \\ $$
Answered by mind is power last updated on 15/Dec/19
![2F_1 (a,b,c,z)=Σ((a_i b_i )/c_i )(z^i /(i!)) 2F_1 (1,((n+1)/2),((n+3)/2),2(√2)−3)=1+Σ_(k≥1) ((1....(k)×(((n+1)/2))....(((n+1)/2)+k−1))/(((n+3)/2).......(((n+3)/2)+k−1)))(((2(√2)−3)^k )/(k!)) =1+Σ_(k≥1) (((n+1)(2(√2)−3)^j )/((n+3+2k−2))). Σ_(n=0) ^(+∞) (((−1)^n ((√2)−1)^n 2F1(1,((n+1)/2),((n+3)/2),2(√2)−3))/(n+1))=Σ_(n≥0) (((−1)^n ((√2)−1)^n .{1+Σ_(k≥1) (((n+1)(2(√2)−3)^k )/(n+1+2k)))/(n+1)) S=Σ_(n≥0) (((−1)^n ((√2)−1)^n )/(n+1))+Σ_(n≥0) (((−1)^n ((√2)−1)^n .Σ_(k≥1) (((n+1)(2(√2)−3)^k )/(n+1+2k)))/(n+1)) let S_1 =Σ_(n≥0) (((−1)^n .((√2)−1)^n )/(n+1)),S_2 =Σ_(n≥0) (((−1)^n ((√2)−1)^n Σ_(k≥1) (((n+1)(2(√2)−3)^k )/(n+1+2k)))/(n+1)) S_2 =Σ_(n≥0) (−1)^n ((√2)−1)^n .Σ_(k≥1) (((2(√2)−3)^k )/(n+1+2k)) (1/(1+x))=Σ_(k≥0) (−x)^k ⇒∫_0 ^((√2)−1) (dx/(1+x))=Σ_(k≥0) ∫_0 ^((√2)−1) (−x)^k dx=Σ_(k≥0) (((−1)^k ((√2)−1)^(k+1) )/(k+1)) ⇒S_1 =(1/( (√2)−1)).∫_0 ^((√2)−1) (dx/(1+x))=((ln((√2)))/( (√2)−1))=((ln(2))/(2((√2)−1))) 2(√2)−3=−((√2)−1)^2 ⇒S_2 =(1/( (√2)−1))Σ_(n≥0) Σ_(k≥1) (((−1)^(n+k) .((√2)−1)^(n+2k+1) )/(n+2k+1)) S_2 =(1/( (√2)−1)).Σ_(n≥0) .Σ_(k≥1) Σ_(k≥1) ((((√2)−1)^(n+2k+1) )/(n+2k+1)) (x^n /(1+x^2 ))=Σ_(k≥0) (−1)^k .x^(2k+n) ⇒∫(((−1)^n x^n )/(1+x^2 ))dx=Σ_(k≥0) ∫(−1)^(k+n) .x^(2k+n) dx=Σ_(k≥1) (((−1)^(k+n) x^(2k+n+1) )/(2k+n+1)) ⇒S′_2 =(1/( (√2)−1))Σ_(n≥0) Σ_(k≥0) (((−1)^(k+n) .((√2)−1)^(n+2k+1) )/(2k+n+1))=(1/( (√2)−1))Σ_(n≥0) .∫_0 ^((√2)−1) (((−x)^n )/(1+x^2 ))dx =(1/( (√2)−1)).∫_0 ^((√2)−1) ((1/(1+x^2 )))Σ_(n≥0) (−x)^n dx =(1/( (√2)−1)).∫_0 ^((√2)−1) .(1/(1+x^2 )).(1/(1+x))dx=(1/( (√2)−1))∫_0 ^((√2)−1) ..(dx/((1+x^2 )(1+x))) (1/((1+x)(1+x^2 )))=(1/2){.(1/(1+x))+((−x+1)/(1+x^2 ))} ∫_0 ^((√2)−1) (1/2){(1/(1+x))−(x/(1+x^2 ))+(1/(1+x^2 ))}dx =(1/2)[ln(x+1)−(1/2)ln(1+x^2 )+arctan(x)]_0 ^((√2)−1) =(1/2).ln((√2))−((ln(1+((√2)−1)^2 ))/4)+((arctan((√2)−1))/2) S_2 ′=(((ln(2))/2)−((ln(4−2(√2)))/4)+((arctan((√2)−1))/2)).(1/( (√2)−1)) S_2 =(S_2 ^′ −Σ_(n≥0) (((−1)^n ((√2)−1)^(n+1) )/(n+1))).(1/( (√2)−1)) Σ_(n≥0) (((−1)^n ((√2)−1)^(n+1) )/((n+1)))=(1/)Σ_(n≥0) (((−1)^n ((√2)−1)^(n+1) )/(n+1)) =(1/( (√2)−1)){ln((√2))} S_2 =(1/( (√(2−1))))(((ln(2))/4)−((ln(4−2(√2)))/4)+((arctan((√2)−1))/2)−ln((√2))) =(1/( (√2)−1))(−((ln(4−2(√2)))/4)−((ln(2))/4)+((arctan((√2)−1))/2)) S=S_1 +S_2 =(1/( (√2)−1)){+((ln(2))/4)−((ln(4−2(√2)))/4)}+((arcran((√2)−1))/(2((√2)−1))) tg((π/4))=1⇒((2tg((π/8)))/(1−tg^2 ((π/8))))=tg((π/4))=1⇒tg((π/8)) root of 1−x^2 −2x=0⇒x=((2−(√8))/(−2)),x=((2+(√8))/(−2)) sin tg((π/8))>0⇒tg((π/8))=((2−(√8))/(−2))=(√2)−1⇒arctan((√2)−1)=(π/8) S=(1/( (√2)−1)){((ln(2))/4)−((ln((√(2+(√2)))−(√(2−(√2)))))/2)}+(π/(16((√2)−1)))](https://www.tinkutara.com/question/Q75664.png)
$$\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{z}\right)=\Sigma\frac{\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{i}} }{\mathrm{c}_{\mathrm{i}} }\frac{\mathrm{z}^{\mathrm{i}} }{\mathrm{i}!} \\ $$$$\mathrm{2F}_{\mathrm{1}} \left(\mathrm{1},\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{n}+\mathrm{3}}{\mathrm{2}},\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)=\mathrm{1}+\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}….\left(\mathrm{k}\right)×\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)….\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}+\mathrm{k}−\mathrm{1}\right)}{\frac{\mathrm{n}+\mathrm{3}}{\mathrm{2}}…….\left(\frac{\mathrm{n}+\mathrm{3}}{\mathrm{2}}+\mathrm{k}−\mathrm{1}\right)}\frac{\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{k}} }{\mathrm{k}!} \\ $$$$=\mathrm{1}+\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{j}} }{\left(\mathrm{n}+\mathrm{3}+\mathrm{2k}−\mathrm{2}\right)}. \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} \mathrm{2F1}\left(\mathrm{1},\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{n}+\mathrm{3}}{\mathrm{2}},\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)}{\mathrm{n}+\mathrm{1}}=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} .\left\{\mathrm{1}+\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{k}} }{\mathrm{n}+\mathrm{1}+\mathrm{2k}}\right.}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{S}=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}+\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} .\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{k}} }{\mathrm{n}+\mathrm{1}+\mathrm{2k}}}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{let}\:\mathrm{S}_{\mathrm{1}} =\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} .\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}},\mathrm{S}_{\mathrm{2}} =\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} \underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{k}} }{\mathrm{n}+\mathrm{1}+\mathrm{2k}}}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{2}} =\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}} .\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right)^{\mathrm{k}} }{\mathrm{n}+\mathrm{1}+\mathrm{2k}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{x}\right)^{\mathrm{k}} \Rightarrow\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}}=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \left(−\mathrm{x}\right)^{\mathrm{k}} \mathrm{dx}=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}.\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}}=\frac{\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}=−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{k}} .\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2k}+\mathrm{1}} }{\mathrm{n}+\mathrm{2k}+\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}.\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}.\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum} \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2k}+\mathrm{1}} }{\mathrm{n}+\mathrm{2k}+\mathrm{1}} \\ $$$$\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{k}} .\mathrm{x}^{\mathrm{2k}+\mathrm{n}} \\ $$$$\Rightarrow\int\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\int\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{n}} .\mathrm{x}^{\mathrm{2k}+\mathrm{n}} \mathrm{dx}=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{n}} \mathrm{x}^{\mathrm{2k}+\mathrm{n}+\mathrm{1}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{S}'_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{n}} .\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2k}+\mathrm{1}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}.\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\left(−\mathrm{x}\right)^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}.\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{x}\right)^{\mathrm{n}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}.\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} .\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }.\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} ..\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{x}\right)} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\left\{.\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}+\frac{−\mathrm{x}+\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right\} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right\}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)+\mathrm{arctan}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)−\frac{\mathrm{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \right)}{\mathrm{4}}+\frac{\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} '=\left(\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{4}}+\frac{\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}}\right).\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{2}} =\left(\mathrm{S}_{\mathrm{2}} ^{'} −\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\right).\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\left\{\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\right\} \\ $$$$\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−\mathrm{1}}}\left(\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{4}}+\frac{\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}}−\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\left(−\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{4}}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}+\frac{\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}}\right) \\ $$$$\mathrm{S}=\mathrm{S}_{\mathrm{1}} +\mathrm{S}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\left\{+\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\frac{\mathrm{ln}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{4}}\right\}+\frac{\mathrm{arcran}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$$$\mathrm{tg}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{1}\Rightarrow\frac{\mathrm{2tg}\left(\frac{\pi}{\mathrm{8}}\right)}{\mathrm{1}−\mathrm{tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)}=\mathrm{tg}\left(\frac{\pi}{\mathrm{4}}\right)=\mathrm{1}\Rightarrow\mathrm{tg}\left(\frac{\pi}{\mathrm{8}}\right)\:\mathrm{root}\:\mathrm{of} \\ $$$$\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{2x}=\mathrm{0}\Rightarrow\mathrm{x}=\frac{\mathrm{2}−\sqrt{\mathrm{8}}}{−\mathrm{2}},\mathrm{x}=\frac{\mathrm{2}+\sqrt{\mathrm{8}}}{−\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{tg}\left(\frac{\pi}{\mathrm{8}}\right)>\mathrm{0}\Rightarrow\mathrm{tg}\left(\frac{\pi}{\mathrm{8}}\right)=\frac{\mathrm{2}−\sqrt{\mathrm{8}}}{−\mathrm{2}}=\sqrt{\mathrm{2}}−\mathrm{1}\Rightarrow\mathrm{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\frac{\pi}{\mathrm{8}} \\ $$$$\mathrm{S}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\left\{\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\frac{\mathrm{ln}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\right)}{\mathrm{2}}\right\}+\frac{\pi}{\mathrm{16}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by aliesam last updated on 15/Dec/19

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mind is power last updated on 16/Dec/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
