Question-75743

Facebook Tweet Pin

Question Number 75743 by Master last updated on 16/Dec/19

Commented by Master last updated on 16/Dec/19

$$\mathrm{work}\:\mathrm{without}\:\mathrm{lopart} \\ $$

Commented by $@ty@m123 last updated on 16/Dec/19

$${What}\:{is}\:{meant}\:{by}\:{lopart}? \\ $$

Commented by abdomathmax last updated on 22/Dec/19

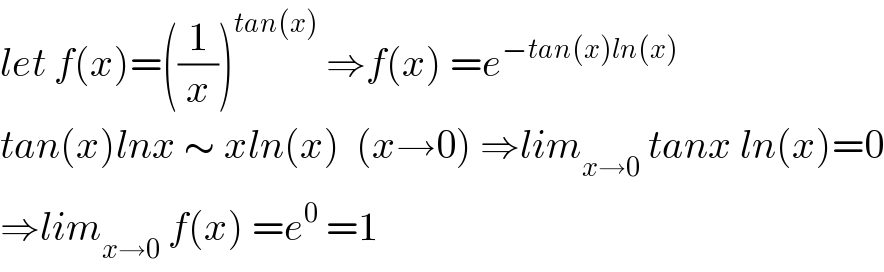
let f(x)=((1/x))^(tan(x)) ⇒f(x) =e^(−tan(x)ln(x)) tan(x)lnx ∼ xln(x) (x→0) ⇒lim_(x→0) tanx ln(x)=0 ⇒lim_(x→0) f(x) =e^0 =1

$${let}\:{f}\left({x}\right)=\left(\frac{\mathrm{1}}{{x}}\right)^{{tan}\left({x}\right)} \:\Rightarrow{f}\left({x}\right)\:={e}^{−{tan}\left({x}\right){ln}\left({x}\right)} \\ $$$${tan}\left({x}\right){lnx}\:\sim\:{xln}\left({x}\right)\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{tanx}\:{ln}\left({x}\right)=\mathrm{0} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)\:={e}^{\mathrm{0}} \:=\mathrm{1} \\ $$

Answered by mr W last updated on 16/Dec/19

lim_(x→0) ((1/x))^x =1 ⇒see Q#75694 lim_(x→0) ((1/x))^(tan x) =lim_(x→0) [((1/x))^x ]^((tan x)/x) =(1)^1 =1 similarly lim_(x→0) ((1/x))^(sin x) =lim_(x→0) [((1/x))^x ]^((sin x)/x) =(1)^1 =1

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{{x}} =\mathrm{1}\:\Rightarrow{see}\:{Q}#\mathrm{75694} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{tan}\:{x}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{\mathrm{1}}{{x}}\right)^{{x}} \right]^{\frac{\mathrm{tan}\:{x}}{{x}}} =\left(\mathrm{1}\right)^{\mathrm{1}} =\mathrm{1} \\ $$$$ \\ $$$${similarly} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{sin}\:{x}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{\mathrm{1}}{{x}}\right)^{{x}} \right]^{\frac{\mathrm{sin}\:{x}}{{x}}} =\left(\mathrm{1}\right)^{\mathrm{1}} =\mathrm{1} \\ $$

Commented by Master last updated on 16/Dec/19

$$\mathrm{thanks} \\ $$

Answered by benjo last updated on 22/Dec/19

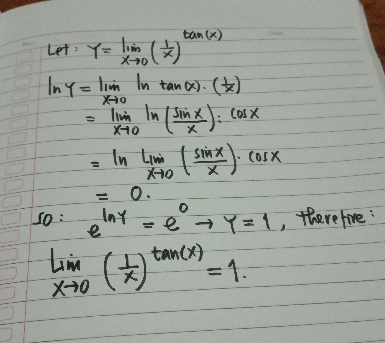
Commented by mr W last updated on 22/Dec/19

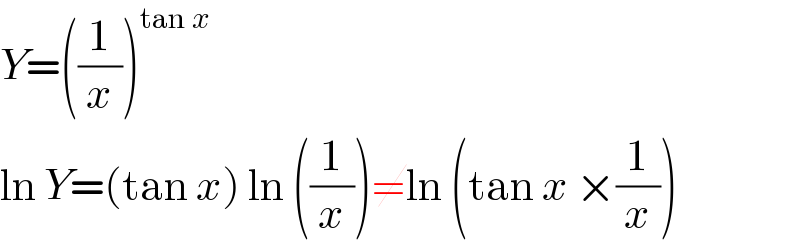
Y=((1/x))^(tan x) ln Y=(tan x) ln ((1/x))≠ln (tan x ×(1/x))

$${Y}=\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{tan}\:{x}} \\ $$$$\mathrm{ln}\:{Y}=\left(\mathrm{tan}\:{x}\right)\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\right)\neq\mathrm{ln}\:\left(\mathrm{tan}\:{x}\:×\frac{\mathrm{1}}{{x}}\right) \\ $$

Commented by john santuy last updated on 24/Dec/19

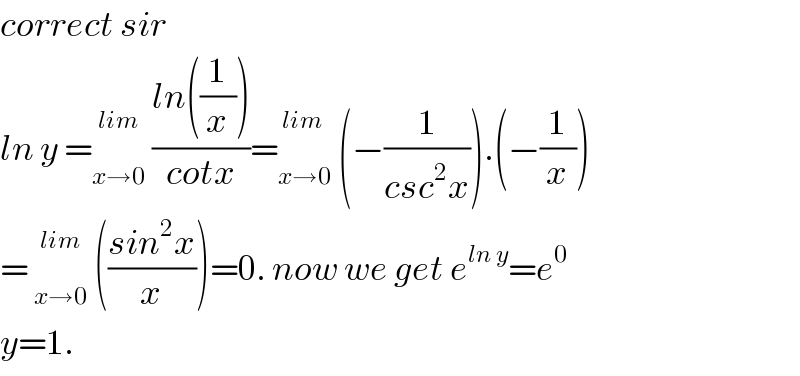
correct sir ln y = _(x→0) ^(lim) ((ln((1/x)))/(cotx))= _(x→0) ^(lim ) (−(1/(csc^2 x))).(−(1/x)) = _(x→0) ^(lim) (((sin^2 x)/x))=0. now we get e^(ln y) =e^0 y=1.

$${correct}\:{sir} \\ $$$${ln}\:{y}\:=\underset{{x}\rightarrow\mathrm{0}} {\overset{{lim}} {\:}}\:\frac{{ln}\left(\frac{\mathrm{1}}{{x}}\right)}{{cotx}}=\underset{{x}\rightarrow\mathrm{0}} {\overset{{lim}\:} {\:}}\:\left(−\frac{\mathrm{1}}{{csc}^{\mathrm{2}} {x}}\right).\left(−\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\overset{{lim}} {\:}}\:\left(\frac{{sin}^{\mathrm{2}} {x}}{{x}}\right)=\mathrm{0}.\:{now}\:{we}\:{get}\:{e}^{{ln}\:{y}} ={e}^{\mathrm{0}} \\ $$$${y}=\mathrm{1}.\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply