Question Number 75783 by mr W last updated on 17/Dec/19

Commented by mr W last updated on 17/Dec/19

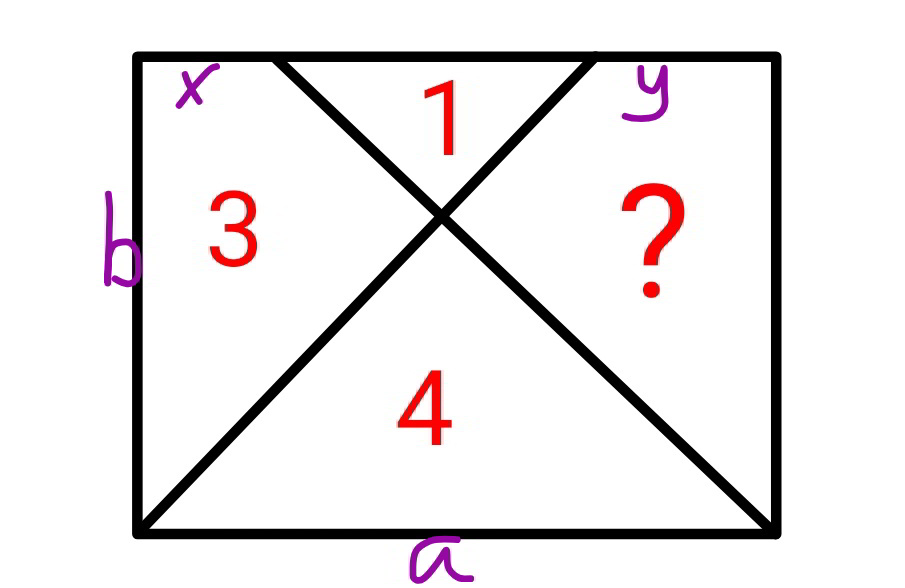
$${find}\:{the}\:{area}\:{missing}. \\ $$
Answered by mr W last updated on 17/Dec/19
Commented by mr W last updated on 17/Dec/19

$${rectangle}={a}×{b} \\ $$$${missing}\:{area}\:?={A} \\ $$$$\frac{{b}\left({a}+{x}\right)}{\mathrm{2}}=\mathrm{4}+\mathrm{3}=\mathrm{7} \\ $$$$\Rightarrow{b}\left({a}+{x}\right)=\mathrm{14}\:\:\:…\left({i}\right) \\ $$$$\frac{{b}\left({a}+{y}\right)}{\mathrm{2}}=\mathrm{4}+{A} \\ $$$$\Rightarrow{b}\left({a}+{y}\right)=\mathrm{8}+\mathrm{2}{A}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${b}\left(\mathrm{2}{a}+{x}+{y}\right)=\mathrm{22}+\mathrm{2}{A} \\ $$$$\frac{{a}−{x}−{y}}{{a}}=\sqrt{\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}+{y}=\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow{b}\left(\mathrm{2}{a}+\frac{{a}}{\mathrm{2}}\right)=\mathrm{22}+\mathrm{2}{A} \\ $$$$\Rightarrow\frac{\mathrm{5}{ba}}{\mathrm{2}}=\mathrm{22}+\mathrm{2}{A} \\ $$$${ba}=\mathrm{1}+\mathrm{3}+\mathrm{4}+{A}=\mathrm{8}+{A} \\ $$$$\Rightarrow\frac{\mathrm{5}\left(\mathrm{8}+{A}\right)}{\mathrm{2}}=\mathrm{22}+\mathrm{2}{A} \\ $$$$\Rightarrow\mathrm{40}+\mathrm{5}{A}=\mathrm{44}+\mathrm{4}{A} \\ $$$$\Rightarrow{A}=\mathrm{4} \\ $$
