Question Number 75830 by Master last updated on 18/Dec/19
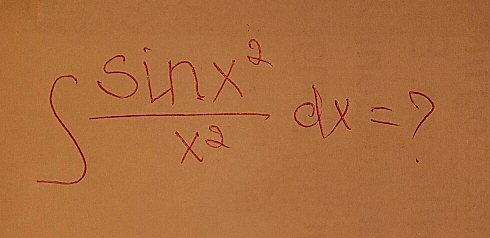
Commented by Master last updated on 18/Dec/19
$$\mathrm{sir}\:\mathrm{mind}\:\mathrm{is}\:\mathrm{power}\:,\:\mathrm{sir}\:\mathrm{mathmax}\:\mathrm{plz} \\ $$
Commented by turbo msup by abdo last updated on 18/Dec/19
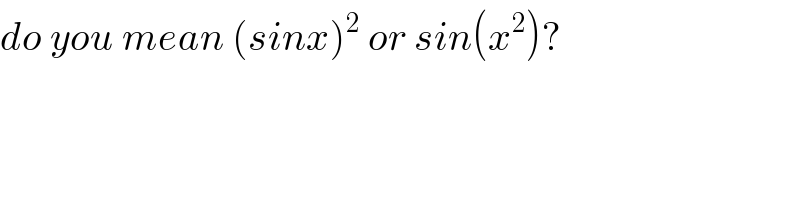
$${do}\:{you}\:{mean}\:\left({sinx}\right)^{\mathrm{2}} \:{or}\:{sin}\left({x}^{\mathrm{2}} \right)? \\ $$
Commented by Master last updated on 18/Dec/19

$$\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$
Commented by mathmax by abdo last updated on 19/Dec/19
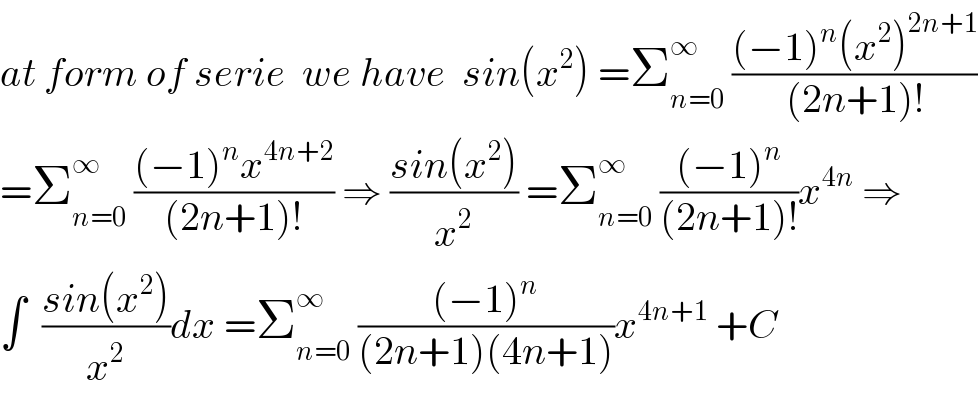
$${at}\:{form}\:{of}\:{serie}\:\:{we}\:{have}\:\:{sin}\left({x}^{\mathrm{2}} \right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \left({x}^{\mathrm{2}} \right)^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\Rightarrow\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{x}^{\mathrm{4}{n}} \:\Rightarrow \\ $$$$\int\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{4}{n}+\mathrm{1}\right)}{x}^{\mathrm{4}{n}+\mathrm{1}} \:+{C}\: \\ $$
Commented by abdomathmax last updated on 19/Dec/19
![let f(x)=∫_0 ^x ((sin(t^2 ))/t^2 )dt ⇒ f(x)=[−((sin(t^2 ))/t)]_0 ^x −∫_0 ^x (−(1/t))(2t cos(t^2 )dt =−((sin(x^2 ))/x) +2 ∫_0 ^x cos(t^2 )dt ∫_0 ^x cos(t^2 )dt =Re(∫_0 ^x e^(−it^2 ) dt) and changement it^2 =u give t^2 =−iu ⇒t =(−iu)^(1/2) ⇒ dt =(−i)^(1/2) (1/2)u^(−(1/2)) =(1/2)e^(−((iπ)/4)) u^(−(1/2)) ⇒ ∫_0 ^x e^(−it^2 ) dt =(1/2)e^(−((iπ)/4)) ∫_0 ^(ix^2 ) e^(−u) u^(−(1/2)) du ...be continued...](https://www.tinkutara.com/question/Q75891.png)
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\frac{{sin}\left({t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} }{dt}\:\Rightarrow \\ $$$${f}\left({x}\right)=\left[−\frac{{sin}\left({t}^{\mathrm{2}} \right)}{{t}}\right]_{\mathrm{0}} ^{{x}} −\int_{\mathrm{0}} ^{{x}} \left(−\frac{\mathrm{1}}{{t}}\right)\left(\mathrm{2}{t}\:{cos}\left({t}^{\mathrm{2}} \right){dt}\right. \\ $$$$=−\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{{x}} \:{cos}\left({t}^{\mathrm{2}} \right){dt} \\ $$$$\int_{\mathrm{0}} ^{{x}} \:{cos}\left({t}^{\mathrm{2}} \right){dt}\:={Re}\left(\int_{\mathrm{0}} ^{{x}} \:{e}^{−{it}^{\mathrm{2}} } {dt}\right)\:\:{and}\:\:{changement} \\ $$$${it}^{\mathrm{2}} ={u}\:{give}\:{t}^{\mathrm{2}} =−{iu}\:\Rightarrow{t}\:=\left(−{iu}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow \\ $$$${dt}\:=\left(−{i}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:{e}^{−{it}^{\mathrm{2}} } {dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{{ix}^{\mathrm{2}} } \:\:{e}^{−{u}} \:\:{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{du} \\ $$$$…{be}\:{continued}… \\ $$
Answered by mr W last updated on 18/Dec/19
![=∫sin x^2 d(−(1/x)) =−((sin x^2 )/x)+2∫cos x^2 dx =−((sin x^2 )/x)+(√(2π))∫cos [(π/2)((((√2)x)/( (√π))))^2 ]d((((√2)x)/( (√π)))) =−((sin x^2 )/x)+(√(2π)) C((((√2)x)/( (√π))))+C with Fresnel integral: S(x)=∫_0 ^x sin (((πt^2 )/2))dt C(x)=∫_0 ^x cos (((πt^2 )/2))dt](https://www.tinkutara.com/question/Q75837.png)
$$=\int\mathrm{sin}\:{x}^{\mathrm{2}} \:{d}\left(−\frac{\mathrm{1}}{{x}}\right) \\ $$$$=−\frac{\mathrm{sin}\:{x}^{\mathrm{2}} }{{x}}+\mathrm{2}\int\mathrm{cos}\:{x}^{\mathrm{2}} {dx} \\ $$$$=−\frac{\mathrm{sin}\:{x}^{\mathrm{2}} }{{x}}+\sqrt{\mathrm{2}\pi}\int\mathrm{cos}\:\left[\frac{\pi}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{\pi}}\right)^{\mathrm{2}} \right]{d}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{\pi}}\right) \\ $$$$=−\frac{\mathrm{sin}\:{x}^{\mathrm{2}} }{{x}}+\sqrt{\mathrm{2}\pi}\:{C}\left(\frac{\sqrt{\mathrm{2}}{x}}{\:\sqrt{\pi}}\right)+{C} \\ $$$${with}\:{Fresnel}\:{integral}: \\ $$$${S}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \mathrm{sin}\:\left(\frac{\pi{t}^{\mathrm{2}} }{\mathrm{2}}\right){dt} \\ $$$${C}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \mathrm{cos}\:\left(\frac{\pi{t}^{\mathrm{2}} }{\mathrm{2}}\right){dt} \\ $$
