Question Number 75901 by Master last updated on 20/Dec/19
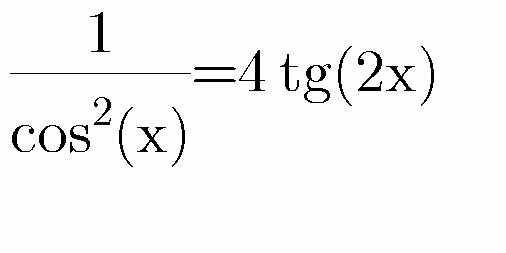
Answered by MJS last updated on 20/Dec/19

$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{4tan}\:\mathrm{2}{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}=\mathrm{2tan}\:\mathrm{2}{x} \\ $$$${x}=\mathrm{arctan}\:{t} \\ $$$$\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{4}{t}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${t}^{\mathrm{4}} +\mathrm{8}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}_{\mathrm{1}} \approx−\mathrm{2}.\mathrm{04004} \\ $$$${t}_{\mathrm{2}} \approx.\mathrm{124970} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} \approx.\mathrm{957536}\pm\mathrm{1}.\mathrm{73366i} \\ $$$$\Rightarrow \\ $$$${x}={n}\pi−\mathrm{1}.\mathrm{11503}\vee{x}={n}\pi+.\mathrm{124325}\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$
Commented by Master last updated on 21/Dec/19
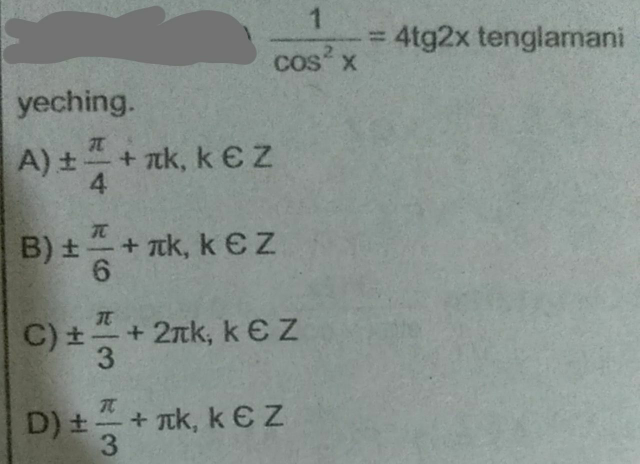
Commented by MJS last updated on 21/Dec/19
$$\mathrm{believe}\:\mathrm{me}\:\mathrm{or}\:\mathrm{not} \\ $$$$\mathrm{try}\:\mathrm{the}\:\mathrm{given}\:\mathrm{options},\:\mathrm{they}\:\mathrm{are}\:\mathrm{all}\:\mathrm{wrong} \\ $$
Commented by MJS last updated on 21/Dec/19

$$\mathrm{I}\:\mathrm{guess}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{4tan}^{\mathrm{2}} \:{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{4}\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:\neq\mathrm{0}\:\Rightarrow\:{x}\neq\frac{\pi}{\mathrm{2}}+{n}\pi \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:{x}\:=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}=\pm\frac{\pi}{\mathrm{6}}+{n}\pi \\ $$
Commented by Master last updated on 21/Dec/19

$$\mathrm{thanks} \\ $$
