Question Number 75902 by Mr. K last updated on 20/Dec/19
Commented by Mr. K last updated on 20/Dec/19
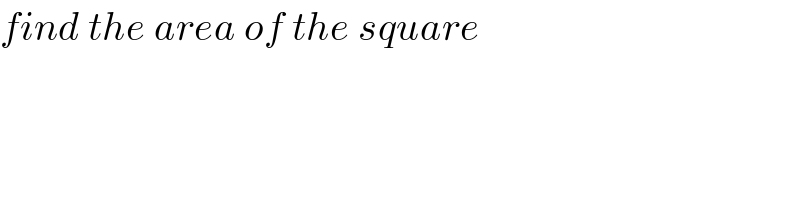
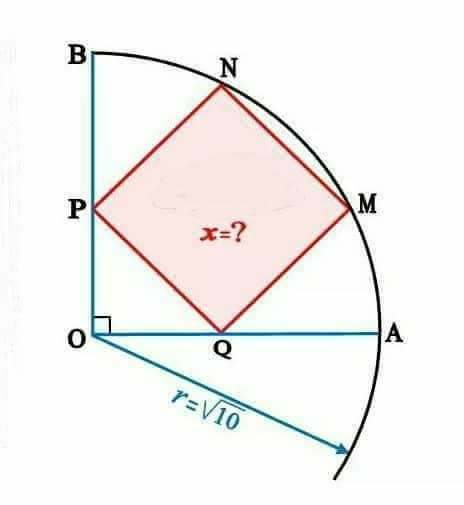
$${find}\:{the}\:{area}\:{of}\:{the}\:{square} \\ $$
Answered by mr W last updated on 20/Dec/19
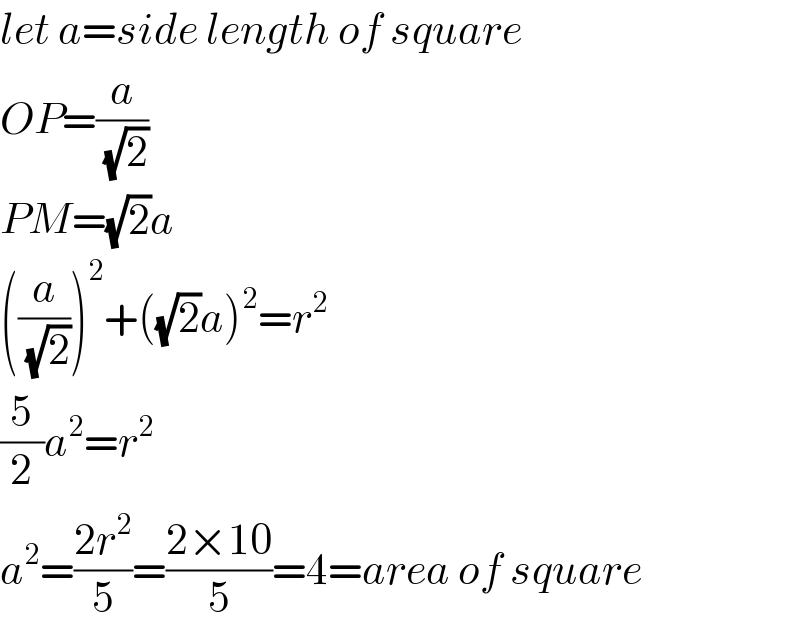
$${let}\:{a}={side}\:{length}\:{of}\:{square} \\ $$$${OP}=\frac{{a}}{\:\sqrt{\mathrm{2}}} \\ $$$${PM}=\sqrt{\mathrm{2}}{a} \\ $$$$\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}{a}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{2}{r}^{\mathrm{2}} }{\mathrm{5}}=\frac{\mathrm{2}×\mathrm{10}}{\mathrm{5}}=\mathrm{4}={area}\:{of}\:{square} \\ $$
Commented by TawaTawa last updated on 22/Dec/19

$$\mathrm{Great}\:\mathrm{sir}. \\ $$$$\mathrm{Please}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{know}\:\mathrm{that}\:\:\angle\mathrm{OPM}\:\:=\:\:\mathrm{90}° \\ $$
Commented by mr W last updated on 22/Dec/19
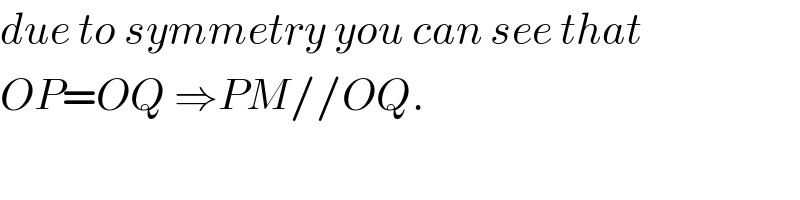
$${due}\:{to}\:{symmetry}\:{you}\:{can}\:{see}\:{that} \\ $$$${OP}={OQ}\:\Rightarrow{PM}//{OQ}. \\ $$
Commented by TawaTawa last updated on 22/Dec/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
