Question-75984

Question Number 75984 by Ajao yinka last updated on 21/Dec/19

Answered by mind is power last updated on 23/Dec/19

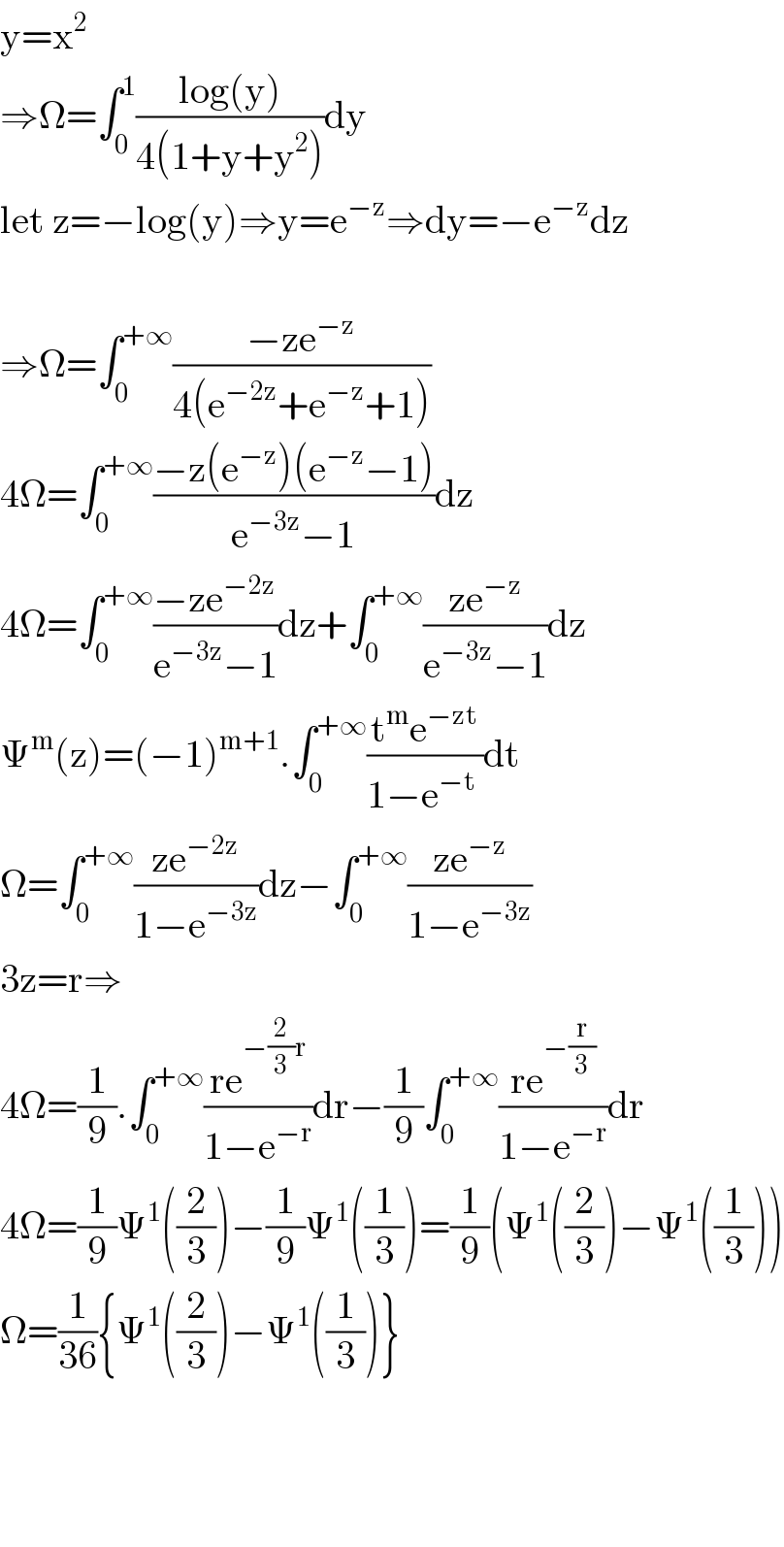
y=x^2 ⇒Ω=∫_0 ^1 ((log(y))/(4(1+y+y^2 )))dy let z=−log(y)⇒y=e^(−z) ⇒dy=−e^(−z) dz ⇒Ω=∫_0 ^(+∞) ((−ze^(−z) )/(4(e^(−2z) +e^(−z) +1))) 4Ω=∫_0 ^(+∞) ((−z(e^(−z) )(e^(−z) −1))/(e^(−3z) −1))dz 4Ω=∫_0 ^(+∞) ((−ze^(−2z) )/(e^(−3z) −1))dz+∫_0 ^(+∞) ((ze^(−z) )/(e^(−3z) −1))dz Ψ^m (z)=(−1)^(m+1) .∫_0 ^(+∞) ((t^m e^(−zt) )/(1−e^(−t) ))dt Ω=∫_0 ^(+∞) ((ze^(−2z) )/(1−e^(−3z) ))dz−∫_0 ^(+∞) ((ze^(−z) )/(1−e^(−3z) )) 3z=r⇒ 4Ω=(1/9).∫_0 ^(+∞) ((re^(−(2/3)r) )/(1−e^(−r) ))dr−(1/9)∫_0 ^(+∞) ((re^(−(r/3)) )/(1−e^(−r) ))dr 4Ω=(1/9)Ψ^1 ((2/3))−(1/9)Ψ^1 ((1/3))=(1/9)(Ψ^1 ((2/3))−Ψ^1 ((1/3))) Ω=(1/(36)){Ψ^1 ((2/3))−Ψ^1 ((1/3))}

$$\mathrm{y}=\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}\left(\mathrm{y}\right)}{\mathrm{4}\left(\mathrm{1}+\mathrm{y}+\mathrm{y}^{\mathrm{2}} \right)}\mathrm{dy} \\ $$$$\mathrm{let}\:\mathrm{z}=−\mathrm{log}\left(\mathrm{y}\right)\Rightarrow\mathrm{y}=\mathrm{e}^{−\mathrm{z}} \Rightarrow\mathrm{dy}=−\mathrm{e}^{−\mathrm{z}} \mathrm{dz} \\ $$$$ \\ $$$$\Rightarrow\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{−\mathrm{ze}^{−\mathrm{z}} }{\mathrm{4}\left(\mathrm{e}^{−\mathrm{2z}} +\mathrm{e}^{−\mathrm{z}} +\mathrm{1}\right)} \\ $$$$\mathrm{4}\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{−\mathrm{z}\left(\mathrm{e}^{−\mathrm{z}} \right)\left(\mathrm{e}^{−\mathrm{z}} −\mathrm{1}\right)}{\mathrm{e}^{−\mathrm{3z}} −\mathrm{1}}\mathrm{dz} \\ $$$$\mathrm{4}\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{−\mathrm{ze}^{−\mathrm{2z}} }{\mathrm{e}^{−\mathrm{3z}} −\mathrm{1}}\mathrm{dz}+\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ze}^{−\mathrm{z}} }{\mathrm{e}^{−\mathrm{3z}} −\mathrm{1}}\mathrm{dz} \\ $$$$\Psi^{\mathrm{m}} \left(\mathrm{z}\right)=\left(−\mathrm{1}\right)^{\mathrm{m}+\mathrm{1}} .\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{t}^{\mathrm{m}} \mathrm{e}^{−\mathrm{zt}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{t}} \:}\mathrm{dt} \\ $$$$\Omega=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ze}^{−\mathrm{2z}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{3z}} }\mathrm{dz}−\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ze}^{−\mathrm{z}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{3z}} } \\ $$$$\mathrm{3z}=\mathrm{r}\Rightarrow \\ $$$$\mathrm{4}\Omega=\frac{\mathrm{1}}{\mathrm{9}}.\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{re}^{−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{r}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{r}} }\mathrm{dr}−\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{re}^{−\frac{\mathrm{r}}{\mathrm{3}}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{r}} }\mathrm{dr} \\ $$$$\mathrm{4}\Omega=\frac{\mathrm{1}}{\mathrm{9}}\Psi^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{9}}\Psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{9}}\left(\Psi^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{36}}\left\{\Psi^{\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply