Question Number 76203 by Master last updated on 25/Dec/19

Commented by Master last updated on 25/Dec/19
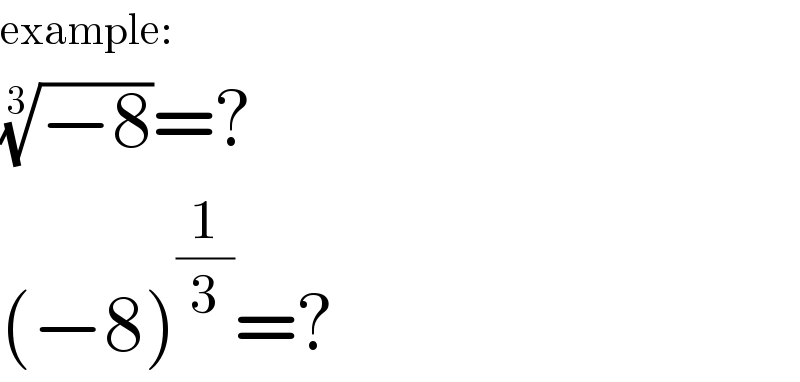
$$\mathrm{example}: \\ $$$$\sqrt[{\mathrm{3}}]{−\mathrm{8}}=? \\ $$$$\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =? \\ $$
Commented by mr W last updated on 25/Dec/19
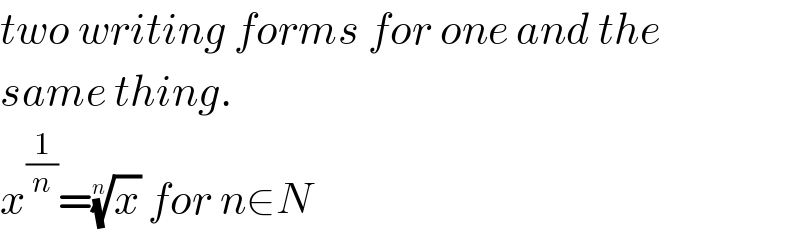
$${two}\:{writing}\:{forms}\:{for}\:{one}\:{and}\:{the} \\ $$$${same}\:{thing}. \\ $$$${x}^{\frac{\mathrm{1}}{{n}}} =\sqrt[{{n}}]{{x}}\:{for}\:{n}\in{N} \\ $$
Commented by Master last updated on 25/Dec/19

$$??? \\ $$
Commented by Master last updated on 25/Dec/19

Commented by Tony Lin last updated on 25/Dec/19

$${how}\:{about}\:{x}^{\frac{\mathrm{2}}{\mathrm{6}}} ? \\ $$$$\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \neq\left(−\mathrm{8}\right)^{\frac{\mathrm{2}}{\mathrm{6}}} \\ $$
Commented by Tony Lin last updated on 25/Dec/19

$${but}\:−\mathrm{8}\neq\mathbb{N} \\ $$
Commented by turbo msup by abdo last updated on 25/Dec/19

$${z}^{\mathrm{3}} =−\mathrm{8}\:\:\:{inside}\:{R}\:{one}\:{solution} \\ $$$$−\mathrm{2}=^{\mathrm{3}} \sqrt{−\mathrm{8}} \\ $$$${inside}\:{C}\:\:\:\:{z}^{\mathrm{3}} +\mathrm{8}=\mathrm{0}\:\Leftrightarrow \\ $$$$\left({z}+\mathrm{2}\right)\left({z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{4}\right)=\mathrm{0}\:\Rightarrow \\ $$$${z}=−\mathrm{2}\:{or}\:{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{4}=\mathrm{0} \\ $$$$\Delta^{'} =\:\mathrm{1}−\mathrm{4}=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$${z}_{\mathrm{1}} =\mathrm{1}+{i}\sqrt{\mathrm{3}}\:{and}\:{z}_{\mathrm{2}} =\mathrm{1}−{i}\sqrt{\mathrm{3}} \\ $$
