Question Number 76326 by Master last updated on 26/Dec/19
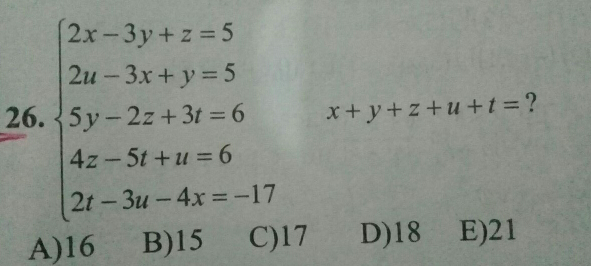
Answered by benjo last updated on 26/Dec/19

$$\mathrm{using}\:\mathrm{determinan}\:\mathrm{Vandermon}\:\mathrm{de}\:\mathrm{method}\: \\ $$
Commented by Master last updated on 26/Dec/19

$$\mathrm{solution}\:\mathrm{plz} \\ $$
Answered by john santu last updated on 26/Dec/19

$$\mathrm{using}\:\mathrm{Crammer}\:\mathrm{rule} \\ $$$$\mathrm{N}\:=\mathrm{661},\:\mathrm{N}_{\mathrm{x}} =\mathrm{1322}\:\rightarrow\mathrm{x}=\frac{\mathrm{1322}}{\mathrm{661}}=\mathrm{2} \\ $$$$\mathrm{N}_{\mathrm{y}} =\mathrm{661},\:\mathrm{y}=\frac{\mathrm{661}}{\mathrm{661}}=\mathrm{1} \\ $$$$\mathrm{N}_{\mathrm{z}} =\mathrm{2644},\:\mathrm{z}=\frac{\mathrm{2644}}{\mathrm{661}}=\mathrm{4} \\ $$$$\mathrm{N}_{\mathrm{u}} =\mathrm{3305},\:\mathrm{u}=\frac{\mathrm{3305}}{\mathrm{661}}=\mathrm{5} \\ $$$$\mathrm{so}\:\mathrm{by}\:\mathrm{substitusi}\:\mathrm{4}\left(\mathrm{4}\right)+\mathrm{5}−\mathrm{6}=\mathrm{5t},\: \\ $$$$\mathrm{t}=\mathrm{3}.\:\mathrm{now}\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:+\mathrm{u}\:+\:\mathrm{t} \\ $$$$=\mathrm{2}+\mathrm{1}+\mathrm{4}+\mathrm{5}+\mathrm{3}=\mathrm{15} \\ $$
Commented by mr W last updated on 26/Dec/19
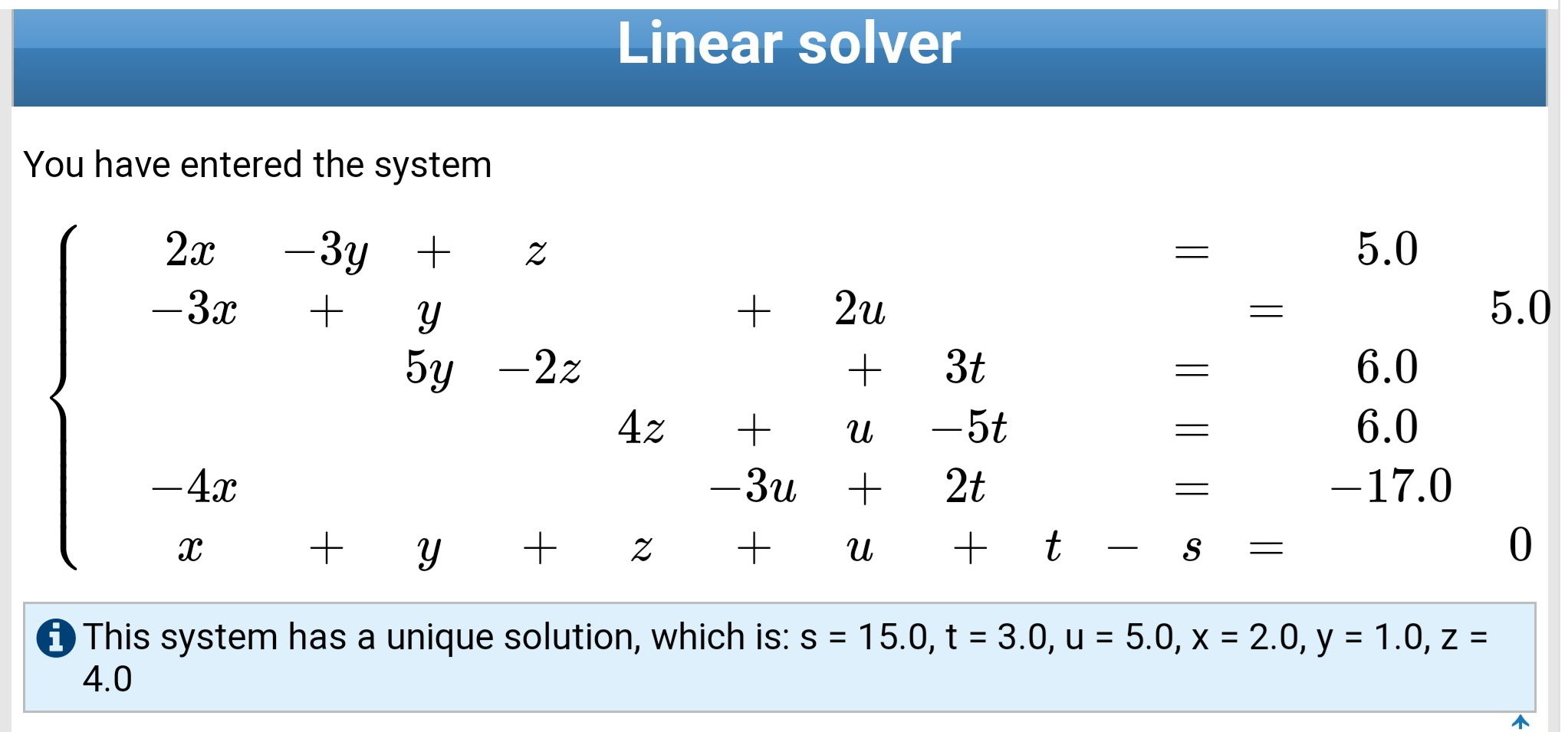
Commented by mr W last updated on 27/Dec/19

$${i}\:{mean}\:{if}\:{we}\:{don}'{t}\:{need}\:{to}\:{know} \\ $$$${the}\:{values}\:{for}\:{x},{y},{z},{u},{t}\:{but}\:{the} \\ $$$${sum}\:{of}\:{them},\:{or}\:{things}\:{like} \\ $$$${x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{4}{u}+\mathrm{5}{t}=?\:{then}\:{we}\:{can}\: \\ $$$${introduce}\:{a}\:{new}\:{unknown}\:{s}\:{and} \\ $$$${add}\:{a}\:{new}\:{equation}\:{like}\:{this}: \\ $$$${x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{4}{u}+\mathrm{5}{t}−{s}=\mathrm{0}\: \\ $$$${now}\:{we}\:{only}\:{need}\:{to}\:{determine}\:{s}: \\ $$$${s}=\frac{{N}_{{s}} }{{N}} \\ $$$$\Rightarrow{x}+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{4}{u}+\mathrm{5}{t}={s}\: \\ $$
Commented by benjo last updated on 27/Dec/19

$$\mathrm{how}\:\mathrm{to}\:\mathrm{find}\:\mathrm{Ns}? \\ $$
Commented by mr W last updated on 27/Dec/19

$${i}\:{assumed}\:{you}\:{know}\:{Cramer}\:{rule}. \\ $$
Commented by mr W last updated on 27/Dec/19

Commented by john santu last updated on 27/Dec/19
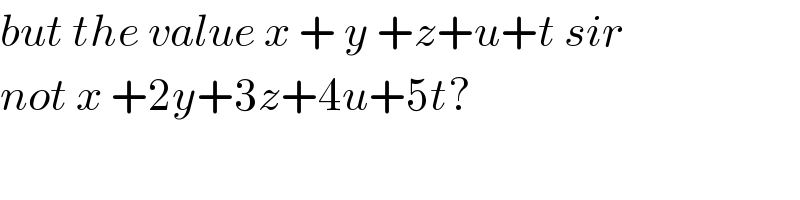
$${but}\:{the}\:{value}\:{x}\:+\:{y}\:+{z}+{u}+{t}\:{sir}\: \\ $$$${not}\:{x}\:+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{4}{u}+\mathrm{5}{t}? \\ $$
Commented by mr W last updated on 27/Dec/19
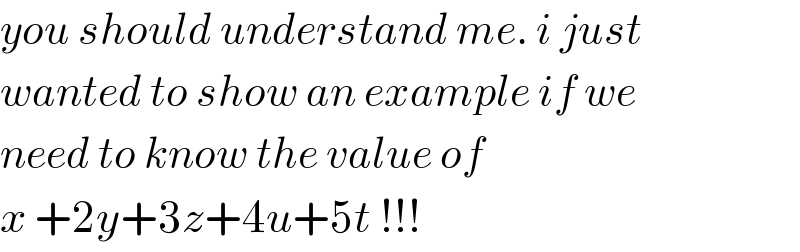
$${you}\:{should}\:{understand}\:{me}.\:{i}\:{just} \\ $$$${wanted}\:{to}\:{show}\:{an}\:{example}\:{if}\:{we} \\ $$$${need}\:{to}\:{know}\:{the}\:{value}\:{of} \\ $$$${x}\:+\mathrm{2}{y}+\mathrm{3}{z}+\mathrm{4}{u}+\mathrm{5}{t}\:!!! \\ $$
