Question Number 76555 by aliesam last updated on 28/Dec/19

Answered by MJS last updated on 28/Dec/19
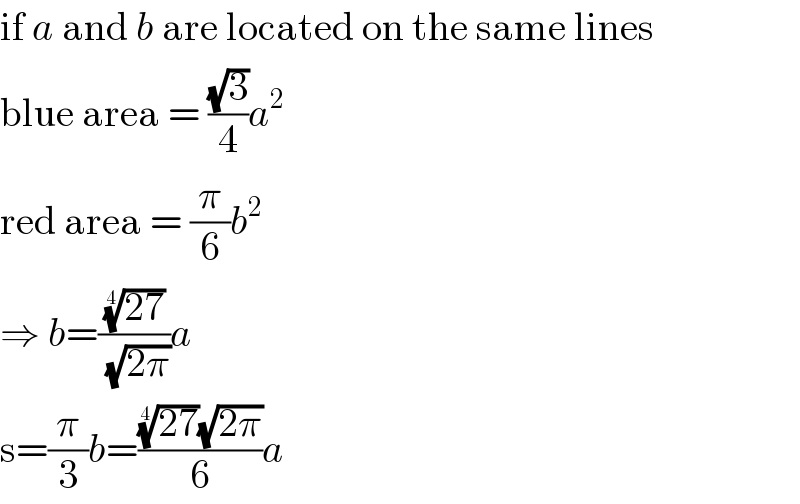
$$\mathrm{if}\:{a}\:\mathrm{and}\:{b}\:\mathrm{are}\:\mathrm{located}\:\mathrm{on}\:\mathrm{the}\:\mathrm{same}\:\mathrm{lines} \\ $$$$\mathrm{blue}\:\mathrm{area}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}^{\mathrm{2}} \\ $$$$\mathrm{red}\:\mathrm{area}\:=\:\frac{\pi}{\mathrm{6}}{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{b}=\frac{\sqrt[{\mathrm{4}}]{\mathrm{27}}}{\:\sqrt{\mathrm{2}\pi}}{a} \\ $$$$\mathrm{s}=\frac{\pi}{\mathrm{3}}{b}=\frac{\sqrt[{\mathrm{4}}]{\mathrm{27}}\sqrt{\mathrm{2}\pi}}{\mathrm{6}}{a} \\ $$
Commented by john santu last updated on 28/Dec/19
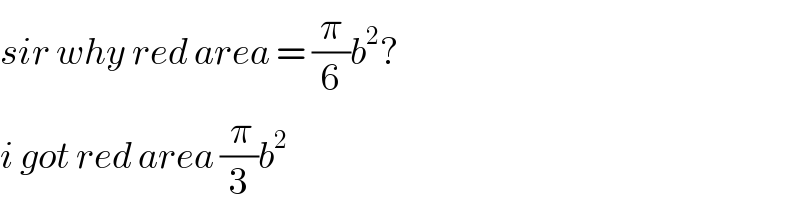
$${sir}\:{why}\:{red}\:{area}\:=\:\frac{\pi}{\mathrm{6}}{b}^{\mathrm{2}} ?\: \\ $$$${i}\:{got}\:{red}\:{area}\:\frac{\:\pi}{\mathrm{3}}{b}^{\mathrm{2}} \\ $$
Commented by benjo 1/2 santuyy last updated on 28/Dec/19

$${good}\:{sir} \\ $$
Commented by benjo 1/2 santuyy last updated on 28/Dec/19

$${correct}\:{sir}\:.\:{red}\:{area}\:=\:\left(\mathrm{1}/\mathrm{2}\right)\left(\:\pi/\mathrm{3}\:\right){b}^{\mathrm{2}} \: \\ $$
Commented by vishalbhardwaj last updated on 28/Dec/19

$$\mathrm{sir}\:\mathrm{MJS}\:,\mathrm{which}\:\mathrm{book}\:\mathrm{is}\:\mathrm{excellent}\:\mathrm{for} \\ $$$$\mathrm{teaching}\:\mathrm{to}\:\mathrm{comptitiveclasses} \\ $$
