Question Number 76587 by Master last updated on 28/Dec/19

Commented by Master last updated on 28/Dec/19

$$\mathrm{sir}\:\mathrm{mind}\:\mathrm{is}\:\mathrm{power} \\ $$
Commented by Master last updated on 28/Dec/19
![#correction Problem 7 the function f is an absolute continuous on [a;b]](https://www.tinkutara.com/question/Q76610.png)
$$#\mathrm{correction} \\ $$$$\mathrm{Problem}\:\mathrm{7} \\ $$$$\mathrm{the}\:\mathrm{function}\:\mathrm{f}\:\mathrm{is}\:\mathrm{an}\:\mathrm{absolute}\:\mathrm{continuous} \\ $$$$\mathrm{on}\:\left[\mathrm{a};\mathrm{b}\right] \\ $$
Commented by Master last updated on 28/Dec/19

$$\mathrm{sir}\:\:\mathrm{W} \\ $$
Answered by mr W last updated on 29/Dec/19

Commented by mr W last updated on 29/Dec/19
![AB=40 EF=41((√3)−1) side length of square =a (a/(sin 120°))=((AB)/(sin (60°−α))) sin (60°−α)=((20(√3))/a) ⇒α=60°−sin^(−1) ((20(√3))/a) sin α=((√3)/2)×((√(a^2 −1200))/a)−(1/2)×((20(√3))/a)=(((√(3(a^2 −1200)))−20(√3))/(2a)) cos α=(1/2)×((√(a^2 −1200))/a)+((√3)/2)×((20(√3))/a)=(((√(a^2 −1200))+60)/(2a)) ((EZ)/(sin α))=((ZY)/(sin 120°))=((2a)/( (√3))) ⇒EZ=((2a sin α)/( (√3))) ((FZ)/(sin (30°−α)))=((ZA)/(sin 120°))=((2a)/( (√3))) ⇒FZ=((2a sin (30°−α))/( (√3))) EZ+FZ=41((√3)−1) ⇒((2a[sin α+sin (30°−α)])/( (√3)))=41((√3)−1) ⇒sin α+sin (30°−α)=((41(3−(√3)))/(2a)) ⇒(1−((√3)/2))sin α+(1/2) cos α=((41(3−(√3)))/(2a)) ⇒(2−(√3))sin α+cos α=((41(3−(√3)))/a) ⇒(2−(√3))(((√(3(a^2 −1200)))−20(√3))/(2a))+(((√(a^2 −1200))+60)/(2a))=((41(3−(√3)))/a) ⇒(2−(√3))(√(3(a^2 −1200)))−20(√3)(2−(√3))+(√(a^2 −1200))+60=82(3−(√3)) ⇒(√(a^2 −1200))=21(√3) ⇒a=(√(1200+(21(√3))^2 ))=29(√3)≈50.23](https://www.tinkutara.com/question/Q76679.png)
$${AB}=\mathrm{40} \\ $$$${EF}=\mathrm{41}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$${side}\:{length}\:{of}\:{square}\:={a} \\ $$$$\frac{{a}}{\mathrm{sin}\:\mathrm{120}°}=\frac{{AB}}{\mathrm{sin}\:\left(\mathrm{60}°−\alpha\right)} \\ $$$$\mathrm{sin}\:\left(\mathrm{60}°−\alpha\right)=\frac{\mathrm{20}\sqrt{\mathrm{3}}}{{a}} \\ $$$$\Rightarrow\alpha=\mathrm{60}°−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{20}\sqrt{\mathrm{3}}}{{a}} \\ $$$$\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}}{{a}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{20}\sqrt{\mathrm{3}}}{{a}}=\frac{\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{1200}\right)}−\mathrm{20}\sqrt{\mathrm{3}}}{\mathrm{2}{a}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}}{{a}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{20}\sqrt{\mathrm{3}}}{{a}}=\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}+\mathrm{60}}{\mathrm{2}{a}} \\ $$$$ \\ $$$$\frac{{EZ}}{\mathrm{sin}\:\alpha}=\frac{{ZY}}{\mathrm{sin}\:\mathrm{120}°}=\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{EZ}=\frac{\mathrm{2}{a}\:\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{3}}} \\ $$$$\frac{{FZ}}{\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right)}=\frac{{ZA}}{\mathrm{sin}\:\mathrm{120}°}=\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{FZ}=\frac{\mathrm{2}{a}\:\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right)}{\:\sqrt{\mathrm{3}}} \\ $$$${EZ}+{FZ}=\mathrm{41}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{2}{a}\left[\mathrm{sin}\:\alpha+\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right)\right]}{\:\sqrt{\mathrm{3}}}=\mathrm{41}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\alpha+\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right)=\frac{\mathrm{41}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}{a}} \\ $$$$\Rightarrow\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\mathrm{sin}\:\alpha+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\alpha=\frac{\mathrm{41}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}{a}} \\ $$$$\Rightarrow\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha=\frac{\mathrm{41}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{{a}} \\ $$$$\Rightarrow\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\frac{\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{1200}\right)}−\mathrm{20}\sqrt{\mathrm{3}}}{\mathrm{2}{a}}+\frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}+\mathrm{60}}{\mathrm{2}{a}}=\frac{\mathrm{41}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{{a}} \\ $$$$\Rightarrow\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} −\mathrm{1200}\right)}−\mathrm{20}\sqrt{\mathrm{3}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)+\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}+\mathrm{60}=\mathrm{82}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\sqrt{{a}^{\mathrm{2}} −\mathrm{1200}}=\mathrm{21}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{a}=\sqrt{\mathrm{1200}+\left(\mathrm{21}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{29}\sqrt{\mathrm{3}}\approx\mathrm{50}.\mathrm{23} \\ $$
Commented by mr W last updated on 30/Dec/19
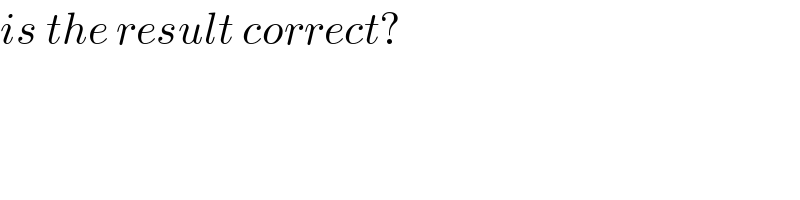
$${is}\:{the}\:{result}\:{correct}? \\ $$
Commented by Master last updated on 30/Dec/19

$$\mathrm{thanks} \\ $$
Commented by mr W last updated on 30/Dec/19
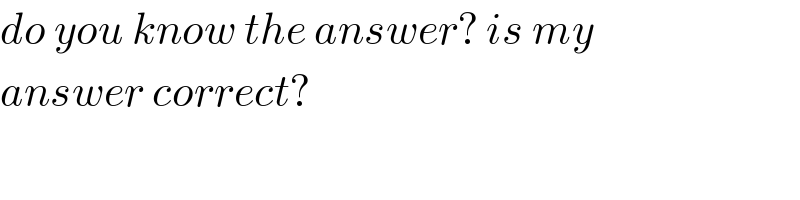
$${do}\:{you}\:{know}\:{the}\:{answer}?\:{is}\:{my} \\ $$$${answer}\:{correct}? \\ $$
