Question Number 76627 by Maclaurin Stickker last updated on 28/Dec/19

Commented by Maclaurin Stickker last updated on 28/Dec/19
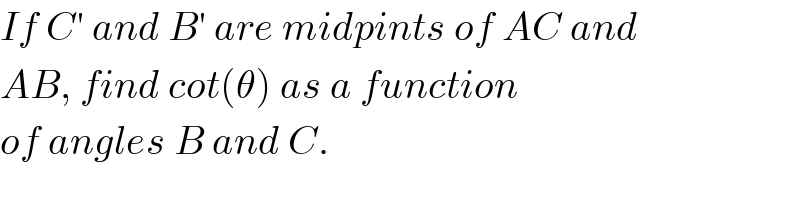
$${If}\:{C}'\:{and}\:{B}'\:{are}\:{midpints}\:{of}\:{AC}\:{and} \\ $$$${AB},\:{find}\:{cot}\left(\theta\right)\:{as}\:{a}\:{function} \\ $$$${of}\:{angles}\:{B}\:{and}\:{C}. \\ $$
Commented by Maclaurin Stickker last updated on 28/Dec/19

$${answer}:\:{cot}\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({cot}\left({B}\right)+{cot}\left({C}\right)\right) \\ $$$${How}\:{can}\:{I}\:{get}\:{this}\:{result}? \\ $$
Answered by $@ty@m123 last updated on 28/Dec/19

$$\mathrm{cot}\:\theta=\frac{{PB}'}{{PM}} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}{B}'{C}'}{{PM}} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}\left({BC}−{B}'{C}'\right)}{{PM}} \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}\left({BM}+{MC}−{C}'{P}−{PB}'\right)}{{PM}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\frac{{BM}−{C}'{P}}{{PM}}\right)+\left(\frac{{MC}−{PB}'}{{PM}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cot}\:{B}+\mathrm{cot}\:{C}\right) \\ $$$$\boldsymbol{{Plese}}\:\boldsymbol{{treat}}\:\boldsymbol{{it}}\:\boldsymbol{{as}}\:\boldsymbol{{a}}\:\boldsymbol{{hint}}\:\boldsymbol{{not}}\:\boldsymbol{{complete}} \\ $$$$\boldsymbol{{solution}}. \\ $$
