Question Number 76663 by aliesam last updated on 29/Dec/19
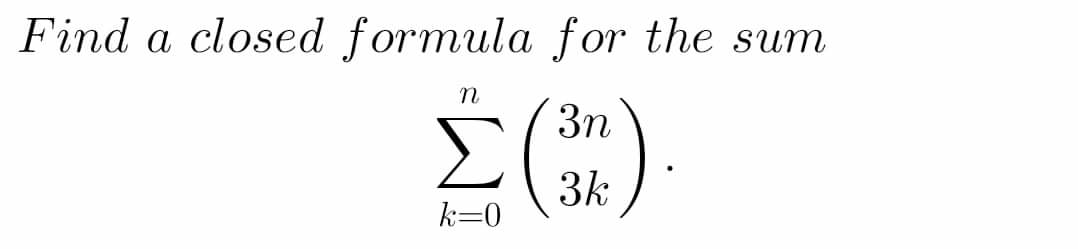
Answered by benjo 1/2 santuyy last updated on 29/Dec/19

$$\mathrm{2}^{\mathrm{3}{n}\:} \:? \\ $$
Answered by mind is power last updated on 29/Dec/19
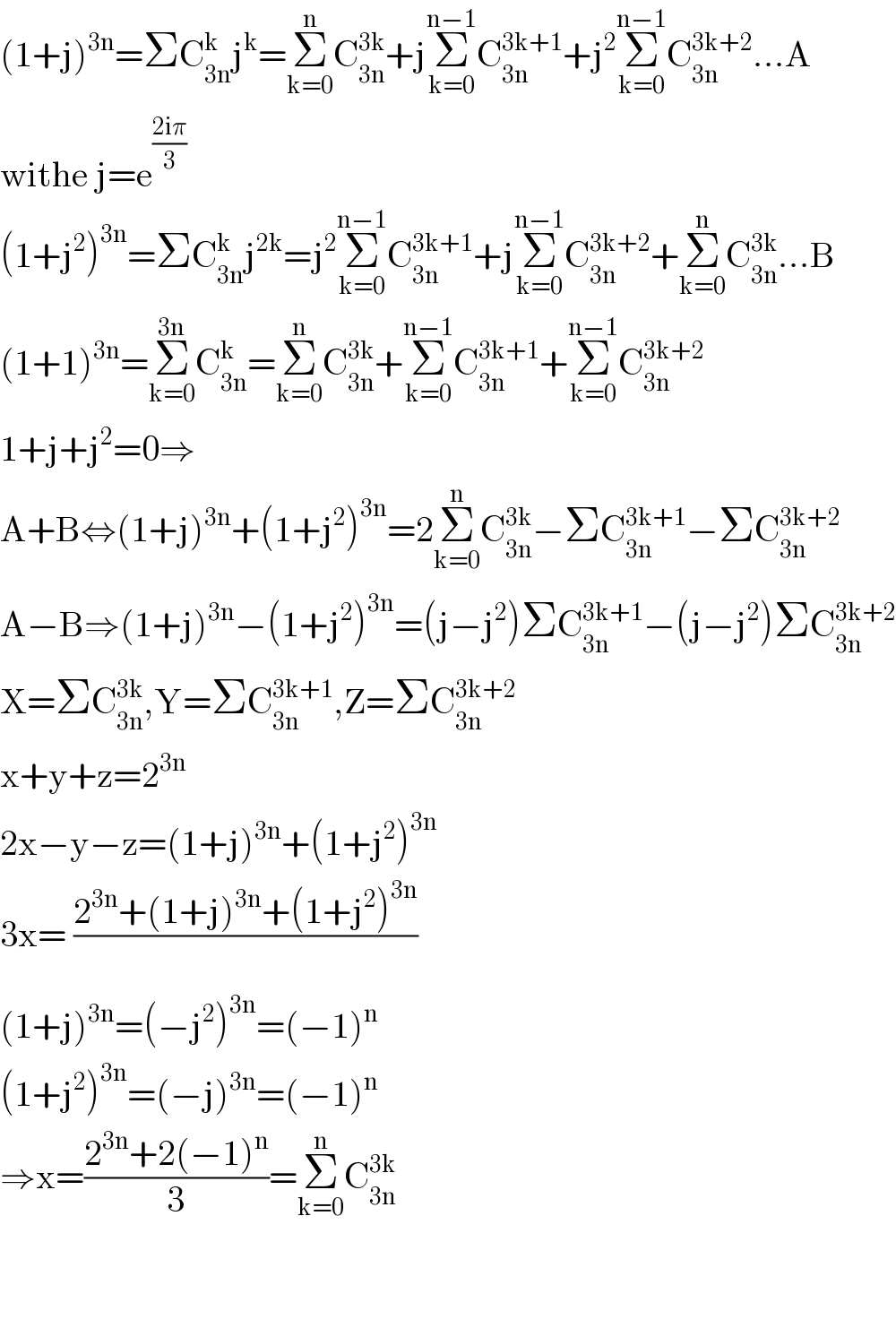
$$\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} =\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{k}} \mathrm{j}^{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} +\mathrm{j}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} +\mathrm{j}^{\mathrm{2}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} …\mathrm{A} \\ $$$$\mathrm{withe}\:\mathrm{j}=\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \\ $$$$\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} =\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{k}} \mathrm{j}^{\mathrm{2k}} =\mathrm{j}^{\mathrm{2}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} +\mathrm{j}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} +\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} …\mathrm{B} \\ $$$$\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{3n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{3n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} +\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} +\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{j}+\mathrm{j}^{\mathrm{2}} =\mathrm{0}\Rightarrow \\ $$$$\mathrm{A}+\mathrm{B}\Leftrightarrow\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} +\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} =\mathrm{2}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} −\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} −\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} \\ $$$$\mathrm{A}−\mathrm{B}\Rightarrow\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} −\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} =\left(\mathrm{j}−\mathrm{j}^{\mathrm{2}} \right)\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} −\left(\mathrm{j}−\mathrm{j}^{\mathrm{2}} \right)\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} \\ $$$$\mathrm{X}=\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} ,\mathrm{Y}=\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{1}} ,\mathrm{Z}=\Sigma\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}+\mathrm{2}} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{2}^{\mathrm{3n}} \\ $$$$\mathrm{2x}−\mathrm{y}−\mathrm{z}=\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} +\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} \\ $$$$\mathrm{3x}=\:\frac{\mathrm{2}^{\mathrm{3n}} +\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} +\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} }{} \\ $$$$\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{3n}} =\left(−\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} =\left(−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$\left(\mathrm{1}+\mathrm{j}^{\mathrm{2}} \right)^{\mathrm{3n}} =\left(−\mathrm{j}\right)^{\mathrm{3n}} =\left(−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{2}^{\mathrm{3n}} +\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3}}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{3n}} ^{\mathrm{3k}} \\ $$$$ \\ $$$$ \\ $$
