Menu Close

Question-7668

Tinku Tara 0 Comments
Pin




Question Number 7668 by 314159 last updated on 08/Sep/16
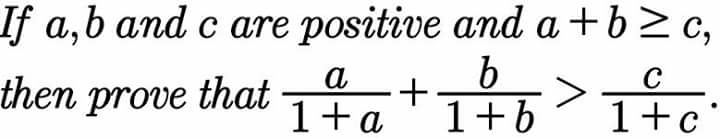
Commented by Yozzia last updated on 08/Sep/16
Suppose a+b=c, with a,b,c>0. Let n=(a/(1+a))+(b/(1+b))−(c/(1+c)). n=(a/(1+a))+(b/(1+b))−((a+b)/(1+a+b)) n=(a/(1+a))−(a/(1+a+b))+(b/(1+b))−(b/(1+a+b)) n=a((1/(1+a))−(1/(1+a+b)))+b((1/(1+b))−(1/(1+a+b))) n=((ab)/((1+a)(1+a+b)))+((ab)/((1+b)(1+a+b))) Since a,b>0⇒ab,(1+a),(1+b),(1+a+b)>0. ⇒n>0⇒(a/(1+a))+(b/(1+b))−(c/(1+c))>0⇒(a/(1+a))+(b/(1+b))>(c/(1+c)) −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Suppose a+b>c, with a,b,c>0. a+b+ab+1>c+ab+1>c+1 ∵ a,b>0. (a+1)(b+1)>c+1 (1/((a+1)(b+1)))<(1/(c+1)) 1−(1/((a+1)(b+1)))>1−(1/(c+1)) ((a+b+ab+1−1)/((a+1)(b+1)))>((c+1−1)/(c+1)) ((a+b+ab)/((a+1)(b+1)))>(c/(c+1)) But, a,b>0⇒a+b+2ab>a+b+ab. ∴((a+b+2ab)/((a+1)(b+1)))>((a+b+ab)/((a+1)(b+1)))>(c/(c+1)) ((a(b+1)+b(a+1))/((a+1)(b+1)))>(c/(c+1)) ((a(b+1))/((a+1)(b+1)))+((b(a+1))/((a+1)(b+1)))>(c/(c+1)) (a/(a+1))+(b/(b+1))>(c/(c+1)) −−−−−−−−−−−−−−−−−−−−−−−−−−−− In all, if a,b,c>0 and a+b≥c, then (a/(a+1))+(b/(b+1))>(c/(c+1)). ////
$${Suppose}\:{a}+{b}={c},\:{with}\:{a},{b},{c}>\mathrm{0}. \\ $$$${Let}\:{n}=\frac{{a}}{\mathrm{1}+{a}}+\frac{{b}}{\mathrm{1}+{b}}−\frac{{c}}{\mathrm{1}+{c}}. \\ $$$${n}=\frac{{a}}{\mathrm{1}+{a}}+\frac{{b}}{\mathrm{1}+{b}}−\frac{{a}+{b}}{\mathrm{1}+{a}+{b}} \\ $$$${n}=\frac{{a}}{\mathrm{1}+{a}}−\frac{{a}}{\mathrm{1}+{a}+{b}}+\frac{{b}}{\mathrm{1}+{b}}−\frac{{b}}{\mathrm{1}+{a}+{b}} \\ $$$${n}={a}\left(\frac{\mathrm{1}}{\mathrm{1}+{a}}−\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}\right)+{b}\left(\frac{\mathrm{1}}{\mathrm{1}+{b}}−\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}}\right) \\ $$$${n}=\frac{{ab}}{\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{a}+{b}\right)}+\frac{{ab}}{\left(\mathrm{1}+{b}\right)\left(\mathrm{1}+{a}+{b}\right)} \\ $$$${Since}\:{a},{b}>\mathrm{0}\Rightarrow{ab},\left(\mathrm{1}+{a}\right),\left(\mathrm{1}+{b}\right),\left(\mathrm{1}+{a}+{b}\right)>\mathrm{0}. \\ $$$$\Rightarrow{n}>\mathrm{0}\Rightarrow\frac{{a}}{\mathrm{1}+{a}}+\frac{{b}}{\mathrm{1}+{b}}−\frac{{c}}{\mathrm{1}+{c}}>\mathrm{0}\Rightarrow\frac{{a}}{\mathrm{1}+{a}}+\frac{{b}}{\mathrm{1}+{b}}>\frac{{c}}{\mathrm{1}+{c}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{a}+{b}>{c},\:{with}\:\:{a},{b},{c}>\mathrm{0}. \\ $$$${a}+{b}+{ab}+\mathrm{1}>{c}+{ab}+\mathrm{1}>{c}+\mathrm{1}\:\:\because\:{a},{b}>\mathrm{0}. \\ $$$$\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)>{c}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}<\frac{\mathrm{1}}{{c}+\mathrm{1}} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\mathrm{1}−\frac{\mathrm{1}}{{c}+\mathrm{1}} \\ $$$$\frac{{a}+{b}+{ab}+\mathrm{1}−\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{c}+\mathrm{1}−\mathrm{1}}{{c}+\mathrm{1}} \\ $$$$\frac{{a}+{b}+{ab}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{c}}{{c}+\mathrm{1}} \\ $$$${But},\:{a},{b}>\mathrm{0}\Rightarrow{a}+{b}+\mathrm{2}{ab}>{a}+{b}+{ab}. \\ $$$$\therefore\frac{{a}+{b}+\mathrm{2}{ab}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{a}+{b}+{ab}}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{c}}{{c}+\mathrm{1}} \\ $$$$\frac{{a}\left({b}+\mathrm{1}\right)+{b}\left({a}+\mathrm{1}\right)}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{c}}{{c}+\mathrm{1}} \\ $$$$\frac{{a}\left({b}+\mathrm{1}\right)}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}+\frac{{b}\left({a}+\mathrm{1}\right)}{\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)}>\frac{{c}}{{c}+\mathrm{1}} \\ $$$$\frac{{a}}{{a}+\mathrm{1}}+\frac{{b}}{{b}+\mathrm{1}}>\frac{{c}}{{c}+\mathrm{1}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${In}\:{all},\:\:{if}\:{a},{b},{c}>\mathrm{0}\:{and}\:{a}+{b}\geqslant{c},\:{then} \\ $$$$\frac{{a}}{{a}+\mathrm{1}}+\frac{{b}}{{b}+\mathrm{1}}>\frac{{c}}{{c}+\mathrm{1}}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\://// \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzia last updated on 08/Sep/16
Suppose that a(n)>0 for ∀n∈N, and Σ_(n=1) ^m a(n)≥a(m+1), m∈N. Is it true that Σ_(n=1) ^m ((a(n))/(a(n)+1))>((a(m+1))/(a(m+1)+1)) ∀m≥2 ? −−−−−−−−−−−−−−−−−−−−−−−− Let p(m) be the proposition that, ∀m≥2, m∈N, that Σ_(n=1) ^m ((a(n))/(a(n)+1))>((a(m+1))/(a(m+1)+1)) for Σ_(n=1) ^m a(n)≥a(m+1) and a(n)>0 ∀n∈N. (1)Let m=2. Then, a(1)+a(2)≥a(3). (1i)Suppose that a(1)+a(2)=a(3) and let q=((a(1))/(a(1)+1))+((a(2))/(a(2)+1))−((a(3))/(a(3)+1)). Then, q=((a(1))/(a(1)+1))+((a(2))/(a(2)+1))−((a(1)+a(2))/(a(1)+a(2)+1)) q=a(1){(1/(a(1)+1))−(1/(a(1)+a(2)+1))}+a(2){(1/(a(2)+1))−(1/(a(1)+a(2)+1))} q=((a(1)a(2))/((a(1)+1)(a(1)+a(2)+1)))+((a(2)a(1))/((a(2)+1)(a(1)+a(2)+1))) Since a(1),a(2)>0⇒ a(1)a(2)>0, a(1)+1>0, a(2)+1>0, a(1)+a(2)+1>0. Hence q>0⇒Σ_(n=1) ^2 ((a(n))/(a(n)+1))−((a(3))/(a(3)+1))>0 or Σ_(n=1) ^2 ((a(n))/(a(n)+1))>((a(3))/(a(3)+1)). (1ii)Suppose that a(1)+a(2)>a(3). Then, a(1)+a(2)+1+a(1)a(2)>a(3)+1+a(1)a(2) ∵ a(1),a(2)>0⇒a(3)+a(1)a(2)+1>a(3)+1 ∴(a(1)+1)(a(2)+1)>a(3)+1 ⇒(1/((a(1)+1)(a(2)+1)))<(1/(a(3)+1)) ⇒1−(1/(a(1)a(2)+a(1)+a(2)+1))>1−(1/(a(3)+1)) ⇒((a(1)a(2)+a(2)+a(1))/((a(1)+1)(a(2)+1)))>((a(3))/(a(3)+1)) ∵ a(1),a(2)>0⇒2a(1)a(2)+a(2)+a(1)>a(1)a(2)+a(2)+a(1) ∴((2a(1)a(2)+a(2)+a(1))/((a(1)+1)(a(2)+1)))>((a(3))/(a(3)+1)) ((a(1)(a(2)+1)+a(2)(a(1)+1))/((a(1)+1)(a(2)+1)))>((a(3))/(a(3)+1)) ⇒Σ_(n=1) ^2 ((a(n))/(a(n)+1))>((a(3))/(a(3)+1)) Therefore p(m) is true when m=2. −−−−−−−−−−−−−−−−−−−−−− Assume p(m) is true when m=k, i.e Σ_(n=1) ^k ((a(n))/(a(n)+1))>((a(k+1))/(a(k+1)+1)) if Σ_(n=1) ^k a(n)≥a(k+1). (2)Let m=k+1. ∴ Σ_(n=1) ^(k+1) a(n)≥a(k+2) (continue)
$${Suppose}\:{that}\:{a}\left({n}\right)>\mathrm{0}\:{for}\:\forall{n}\in\mathbb{N},\:{and} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}{a}\left({n}\right)\geqslant{a}\left({m}+\mathrm{1}\right),\:{m}\in\mathbb{N}.\:{Is}\:{it}\:{true} \\ $$$${that}\:\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}>\frac{{a}\left({m}+\mathrm{1}\right)}{{a}\left({m}+\mathrm{1}\right)+\mathrm{1}}\:\forall{m}\geqslant\mathrm{2}\:? \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Let}\:{p}\left({m}\right)\:{be}\:{the}\:{proposition}\:{that},\:\forall{m}\geqslant\mathrm{2}, \\ $$$${m}\in\mathbb{N},\:{that}\:\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}>\frac{{a}\left({m}+\mathrm{1}\right)}{{a}\left({m}+\mathrm{1}\right)+\mathrm{1}} \\ $$$${for}\:\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}{a}\left({n}\right)\geqslant{a}\left({m}+\mathrm{1}\right)\:{and}\:{a}\left({n}\right)>\mathrm{0}\:\forall{n}\in\mathbb{N}. \\ $$$$\left(\mathrm{1}\right){Let}\:{m}=\mathrm{2}.\:{Then},\:{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)\geqslant{a}\left(\mathrm{3}\right). \\ $$$$\left(\mathrm{1}{i}\right){Suppose}\:{that}\:{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)={a}\left(\mathrm{3}\right)\:{and} \\ $$$${let}\:{q}=\frac{{a}\left(\mathrm{1}\right)}{{a}\left(\mathrm{1}\right)+\mathrm{1}}+\frac{{a}\left(\mathrm{2}\right)}{{a}\left(\mathrm{2}\right)+\mathrm{1}}−\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}}. \\ $$$${Then},\:{q}=\frac{{a}\left(\mathrm{1}\right)}{{a}\left(\mathrm{1}\right)+\mathrm{1}}+\frac{{a}\left(\mathrm{2}\right)}{{a}\left(\mathrm{2}\right)+\mathrm{1}}−\frac{{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)}{{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}} \\ $$$${q}={a}\left(\mathrm{1}\right)\left\{\frac{\mathrm{1}}{{a}\left(\mathrm{1}\right)+\mathrm{1}}−\frac{\mathrm{1}}{{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}}\right\}+{a}\left(\mathrm{2}\right)\left\{\frac{\mathrm{1}}{{a}\left(\mathrm{2}\right)+\mathrm{1}}−\frac{\mathrm{1}}{{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}}\right\} \\ $$$${q}=\frac{{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)}{\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}\right)}+\frac{{a}\left(\mathrm{2}\right){a}\left(\mathrm{1}\right)}{\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}\right)} \\ $$$${Since}\:{a}\left(\mathrm{1}\right),{a}\left(\mathrm{2}\right)>\mathrm{0}\Rightarrow\:{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)>\mathrm{0}, \\ $$$${a}\left(\mathrm{1}\right)+\mathrm{1}>\mathrm{0},\:{a}\left(\mathrm{2}\right)+\mathrm{1}>\mathrm{0},\:{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}>\mathrm{0}. \\ $$$${Hence}\:{q}>\mathrm{0}\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}−\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}}>\mathrm{0}\: \\ $$$${or}\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}>\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}}. \\ $$$$\left(\mathrm{1}{ii}\right){Suppose}\:{that}\:{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)>{a}\left(\mathrm{3}\right). \\ $$$${Then},\:{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}+{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)>{a}\left(\mathrm{3}\right)+\mathrm{1}+{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right) \\ $$$$\because\:{a}\left(\mathrm{1}\right),{a}\left(\mathrm{2}\right)>\mathrm{0}\Rightarrow{a}\left(\mathrm{3}\right)+{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+\mathrm{1}>{a}\left(\mathrm{3}\right)+\mathrm{1} \\ $$$$\therefore\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)>{a}\left(\mathrm{3}\right)+\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)}<\frac{\mathrm{1}}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+{a}\left(\mathrm{1}\right)+{a}\left(\mathrm{2}\right)+\mathrm{1}}>\mathrm{1}−\frac{\mathrm{1}}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$$\Rightarrow\frac{{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+{a}\left(\mathrm{2}\right)+{a}\left(\mathrm{1}\right)}{\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)}>\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$$\because\:{a}\left(\mathrm{1}\right),{a}\left(\mathrm{2}\right)>\mathrm{0}\Rightarrow\mathrm{2}{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+{a}\left(\mathrm{2}\right)+{a}\left(\mathrm{1}\right)>{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+{a}\left(\mathrm{2}\right)+{a}\left(\mathrm{1}\right) \\ $$$$\therefore\frac{\mathrm{2}{a}\left(\mathrm{1}\right){a}\left(\mathrm{2}\right)+{a}\left(\mathrm{2}\right)+{a}\left(\mathrm{1}\right)}{\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)}>\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$$\frac{{a}\left(\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)+{a}\left(\mathrm{2}\right)\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)}{\left({a}\left(\mathrm{1}\right)+\mathrm{1}\right)\left({a}\left(\mathrm{2}\right)+\mathrm{1}\right)}>\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}>\frac{{a}\left(\mathrm{3}\right)}{{a}\left(\mathrm{3}\right)+\mathrm{1}} \\ $$$${Therefore}\:{p}\left({m}\right)\:{is}\:{true}\:{when}\:{m}=\mathrm{2}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Assume}\:{p}\left({m}\right)\:{is}\:{true}\:{when}\:{m}={k}, \\ $$$${i}.{e}\:\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{{a}\left({n}\right)}{{a}\left({n}\right)+\mathrm{1}}>\frac{{a}\left({k}+\mathrm{1}\right)}{{a}\left({k}+\mathrm{1}\right)+\mathrm{1}} \\ $$$${if}\:\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}{a}\left({n}\right)\geqslant{a}\left({k}+\mathrm{1}\right). \\ $$$$\left(\mathrm{2}\right){Let}\:{m}={k}+\mathrm{1}.\:\therefore\:\underset{{n}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\sum}}{a}\left({n}\right)\geqslant{a}\left({k}+\mathrm{2}\right) \\ $$$$\left({continue}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by 314159 last updated on 08/Sep/16
Thanks
$${Thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *