Question Number 76826 by Master last updated on 30/Dec/19

Answered by john santu last updated on 31/Dec/19
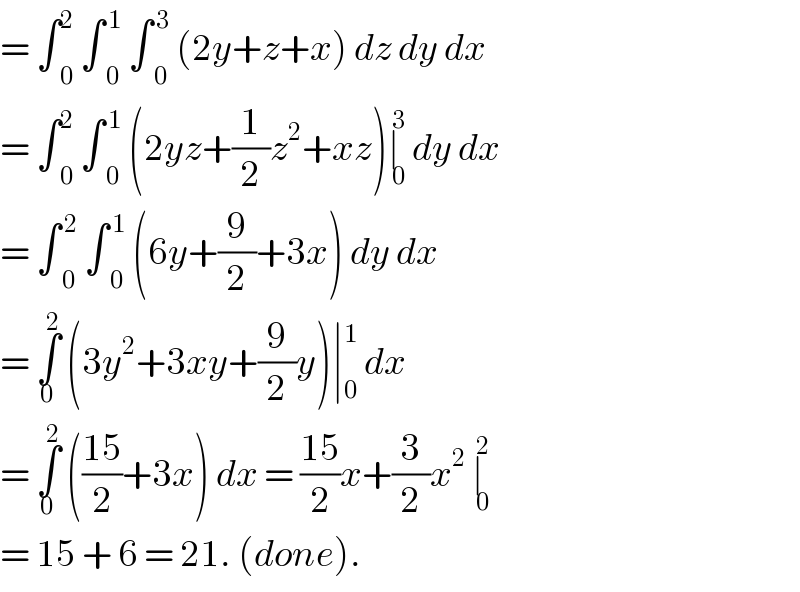
$$=\:\int\underset{\mathrm{0}} {\overset{\mathrm{2}} {\:}}\:\int\underset{\mathrm{0}} {\overset{\:\mathrm{1}} {\:}}\:\int\underset{\mathrm{0}} {\overset{\:\mathrm{3}} {\:}}\:\left(\mathrm{2}{y}+{z}+{x}\right)\:{dz}\:{dy}\:{dx}\: \\ $$$$=\:\int\underset{\mathrm{0}} {\overset{\mathrm{2}} {\:}}\:\int\underset{\mathrm{0}} {\overset{\:\mathrm{1}} {\:}}\:\left(\mathrm{2}{yz}+\frac{\mathrm{1}}{\mathrm{2}}{z}^{\mathrm{2}} +{xz}\right)\underset{\:\mathrm{0}} {\overset{\:\mathrm{3}} {\mid}}\:{dy}\:{dx}\: \\ $$$$=\:\int\underset{\mathrm{0}} {\overset{\:\mathrm{2}} {\:}}\:\int\underset{\mathrm{0}} {\overset{\:\mathrm{1}} {\:}}\:\left(\mathrm{6}{y}+\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{3}{x}\right)\:{dy}\:{dx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\:\mathrm{2}} {\int}}\:\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{3}{xy}+\frac{\mathrm{9}}{\mathrm{2}}{y}\right)\mid\underset{\mathrm{0}} {\overset{\mathrm{1}} {\:}}\:{dx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\left(\frac{\mathrm{15}}{\mathrm{2}}+\mathrm{3}{x}\right)\:{dx}\:=\:\frac{\mathrm{15}}{\mathrm{2}}{x}+\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \:\underset{\:\mathrm{0}} {\overset{\:\mathrm{2}} {\mid}} \\ $$$$=\:\mathrm{15}\:+\:\mathrm{6}\:=\:\mathrm{21}.\:\left({done}\right).\: \\ $$
Commented by Master last updated on 31/Dec/19

$$\mathrm{thanks}\: \\ $$
