Question Number 76910 by aliesam last updated on 31/Dec/19

Commented by MJS last updated on 31/Dec/19
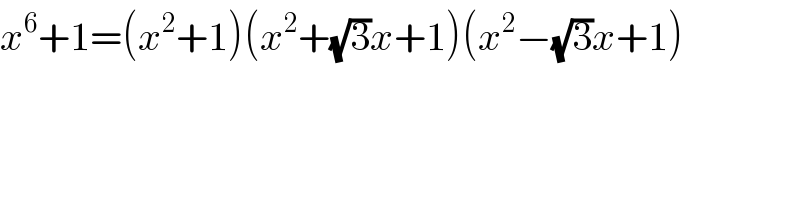
$${x}^{\mathrm{6}} +\mathrm{1}=\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right) \\ $$
Answered by MJS last updated on 01/Jan/20

$$\int\frac{{dx}}{{x}^{\mathrm{6}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\sqrt{\mathrm{3}}{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\sqrt{\mathrm{3}}{x}+\mathrm{2}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx} \\ $$$$\:\:\:\:\:{I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:{x} \\ $$$$\:\:\:\:\:{I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\sqrt{\mathrm{3}}{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\int\frac{\mathrm{2}{x}−\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:{I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\sqrt{\mathrm{3}}{x}+\mathrm{2}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\int\frac{\mathrm{2}{x}+\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right) \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} +{C} \\ $$
