Question Number 76948 by Master last updated on 01/Jan/20

Answered by mr W last updated on 02/Jan/20
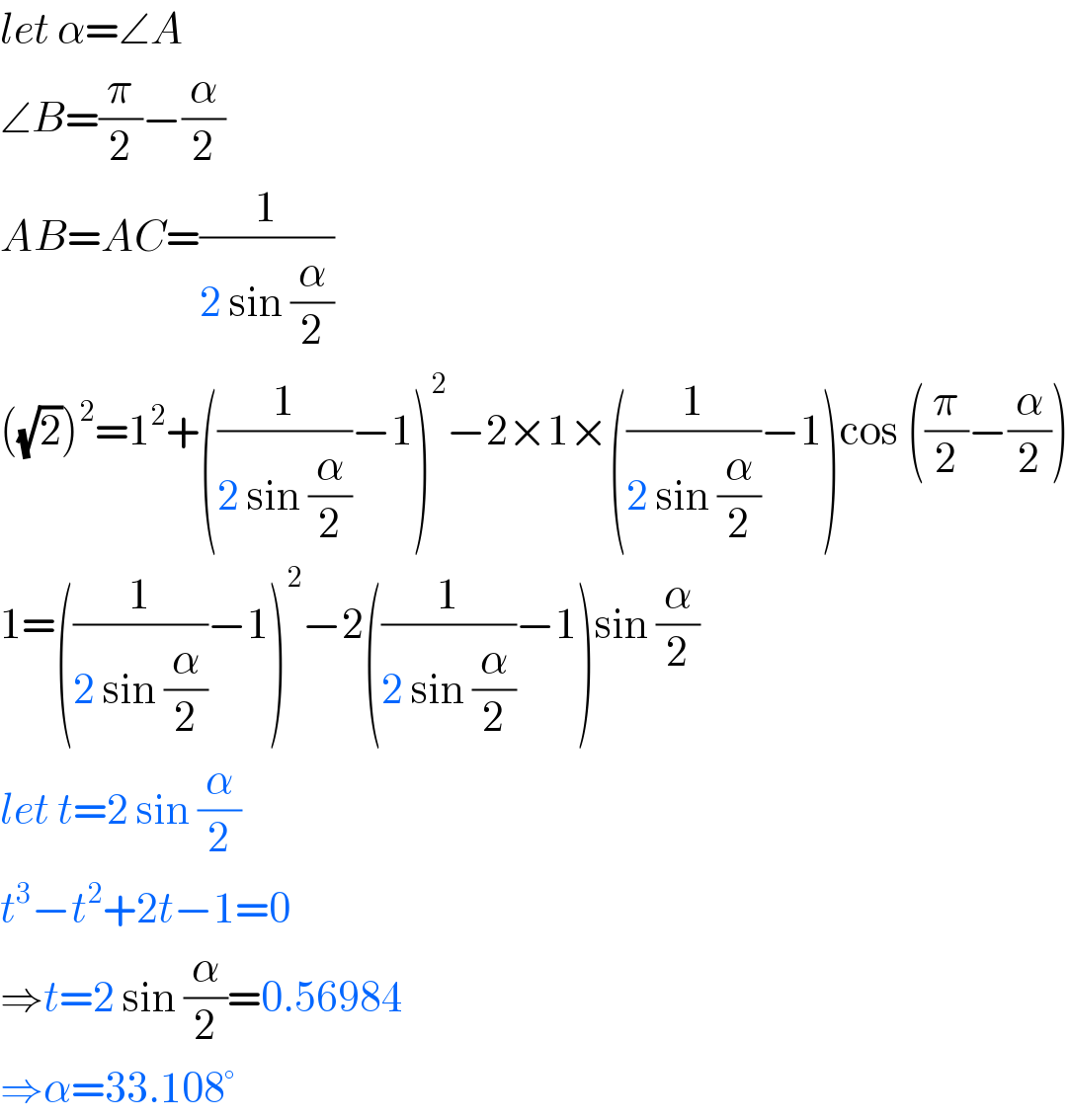
$${let}\:\alpha=\angle{A} \\ $$$$\angle{B}=\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}} \\ $$$${AB}={AC}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}} \\ $$$$\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}−\mathrm{1}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\mathrm{1}=\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}−\mathrm{1}\right)\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$${let}\:{t}=\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\mathrm{0}.\mathrm{56984} \\ $$$$\Rightarrow\alpha=\mathrm{33}.\mathrm{108}° \\ $$
Commented by mr W last updated on 02/Jan/20
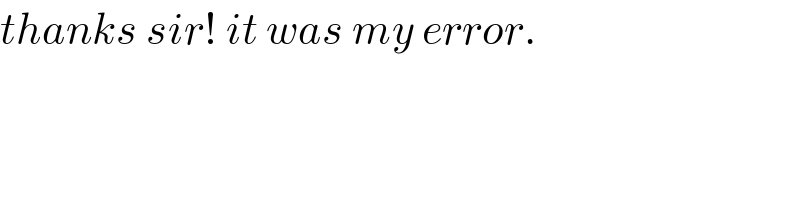
$${thanks}\:{sir}!\:{it}\:{was}\:{my}\:{error}. \\ $$
Commented by $@ty@m123 last updated on 02/Jan/20
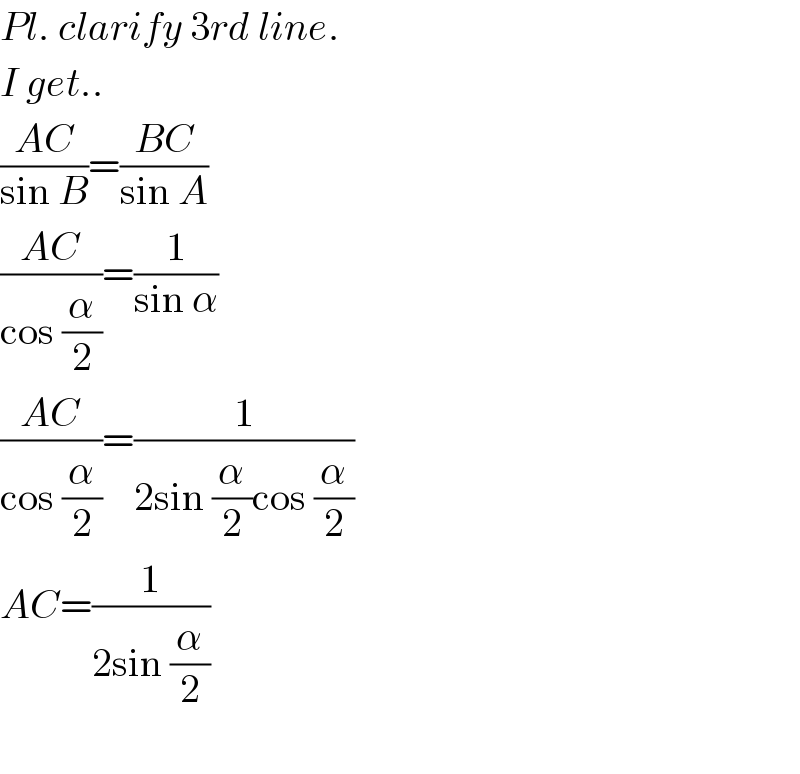
$${Pl}.\:{clarify}\:\mathrm{3}{rd}\:{line}. \\ $$$${I}\:{get}.. \\ $$$$\frac{{AC}}{\mathrm{sin}\:{B}}=\frac{{BC}}{\mathrm{sin}\:{A}} \\ $$$$\frac{{AC}}{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$$$\frac{{AC}}{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}} \\ $$$${AC}=\frac{\mathrm{1}}{\mathrm{2sin}\:\frac{\alpha}{\mathrm{2}}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 29/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
