Question Number 77009 by Master last updated on 02/Jan/20

Commented by Master last updated on 02/Jan/20
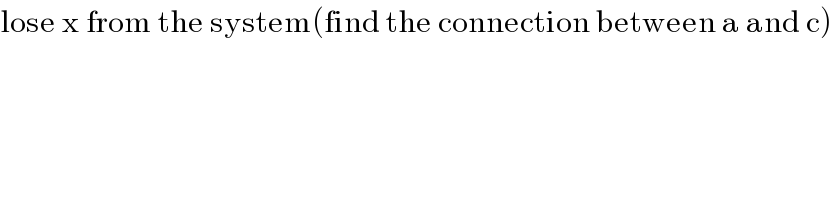
$$\mathrm{lose}\:\mathrm{x}\:\mathrm{from}\:\mathrm{the}\:\mathrm{system}\left(\mathrm{find}\:\mathrm{the}\:\mathrm{connection}\:\mathrm{between}\:\mathrm{a}\:\mathrm{and}\:\mathrm{c}\right) \\ $$
Commented by MJS last updated on 02/Jan/20

$$\mathrm{solve}\:\mathrm{both}\:\mathrm{for}\:{c} \\ $$$${c}=\mathrm{term}_{\mathrm{1}} \:\left({a},\:{x}\right) \\ $$$${c}=\mathrm{term}_{\mathrm{2}} \:\left({a},\:{x}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{term}_{\mathrm{1}} \:\left({a},\:{x}\right)\:=\mathrm{term}_{\mathrm{2}} \:\left({a},\:{x}\right) \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{in}\:{x}^{\mathrm{4}} \&{a}^{\mathrm{4}} \\ $$$$\mathrm{let}\:{x}^{\mathrm{4}} ={y}\wedge{a}^{\mathrm{4}} ={b} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{4}\:\mathrm{exact}\:\mathrm{solutions}\:\mathrm{for}\:{y}\:\mathrm{but}\:\mathrm{they}\:\mathrm{are} \\ $$$$\mathrm{not}\:“\mathrm{nice}''\:\mathrm{and}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{handle} \\ $$$$\Rightarrow \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{insert}\:\mathrm{into}\:{c}=\mathrm{term}_{\mathrm{1}} \:\mathrm{or}\:{c}=\mathrm{term}_{\mathrm{2}} \:\mathrm{and} \\ $$$$\mathrm{get}\:\mathrm{4}\:\mathrm{values}\:\mathrm{for}\:{c}\left({a}\right)\:\mathrm{but}\:\mathrm{again}\:\mathrm{they}\:\mathrm{are}\:\mathrm{not} \\ $$$$“\mathrm{nice}''. \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{willing}\:\mathrm{to}\:\mathrm{type}\:\mathrm{all}\:\mathrm{this},\:\mathrm{do}\:\mathrm{it}\:\mathrm{for} \\ $$$$\mathrm{yourself},\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{but}\:\mathrm{you}'\mathrm{ll}\:\mathrm{waste} \\ $$$$\mathrm{plenty}\:\mathrm{of}\:\mathrm{paper}\:\mathrm{and}\:\mathrm{nerves}… \\ $$
Commented by Master last updated on 02/Jan/20

$$\mathrm{prove}\:\mathrm{that} \\ $$
Commented by MJS last updated on 02/Jan/20

$$\mathrm{prove}\:\mathrm{that}\:\mathrm{for}\:\mathrm{yourself} \\ $$
