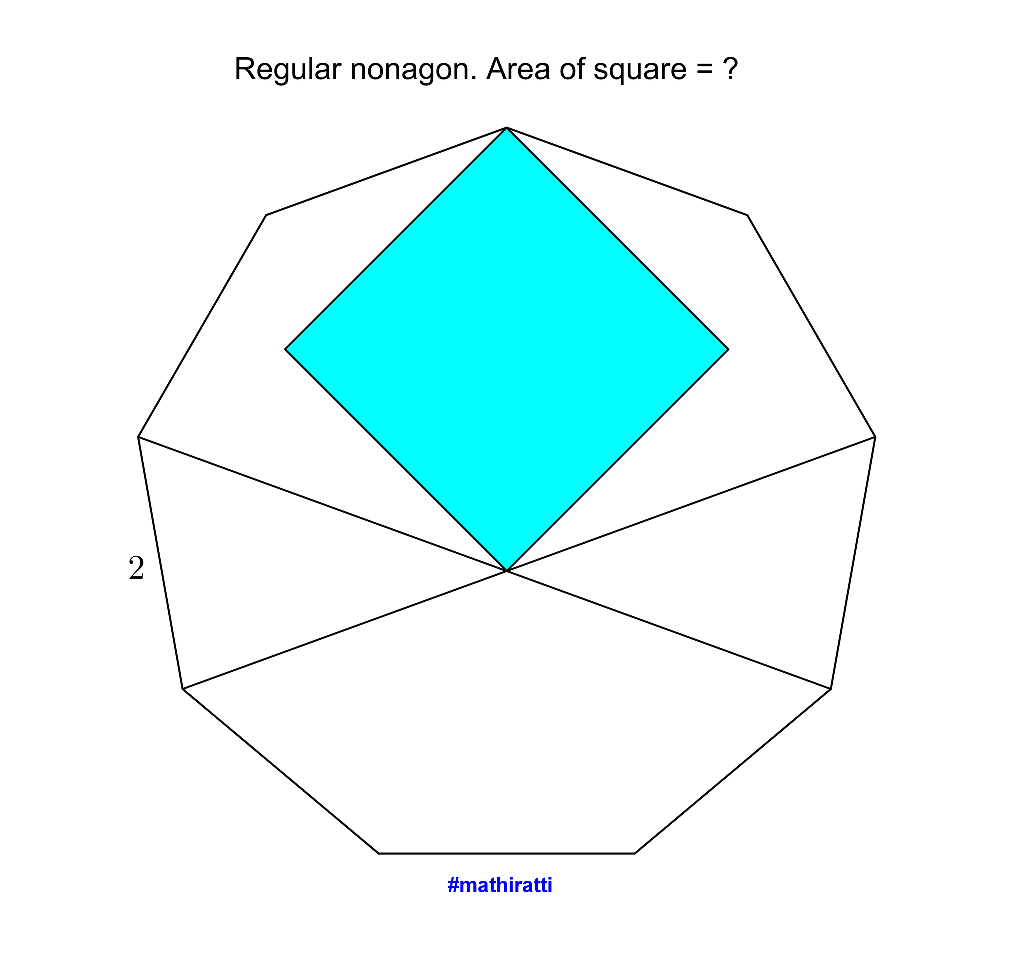
Question Number 77057 by Maclaurin Stickker last updated on 03/Jan/20
Commented by Maclaurin Stickker last updated on 03/Jan/20

$${I}\:{wouldn}'{t}\:{like}\:{an}\:{answer}.\:{I}\:{would}\:{like} \\ $$$${a}\:{tip}\:{on}\:{how}\:{to}\:{solve}\:{this}\:{problem}. \\ $$
Commented by mr W last updated on 03/Jan/20

$${is}\:{the}\:{answer}\:{in}\:{Q}\mathrm{76898}\:{no}\:{help} \\ $$$${for}\:{you}? \\ $$$${also}\:{here}\:{we}\:{should}\:{try}\:{to}\:{determine} \\ $$$${the}\:{length}\:{of}\:{the}\:{diagonal}. \\ $$
Answered by mr W last updated on 03/Jan/20
Commented by mr W last updated on 03/Jan/20

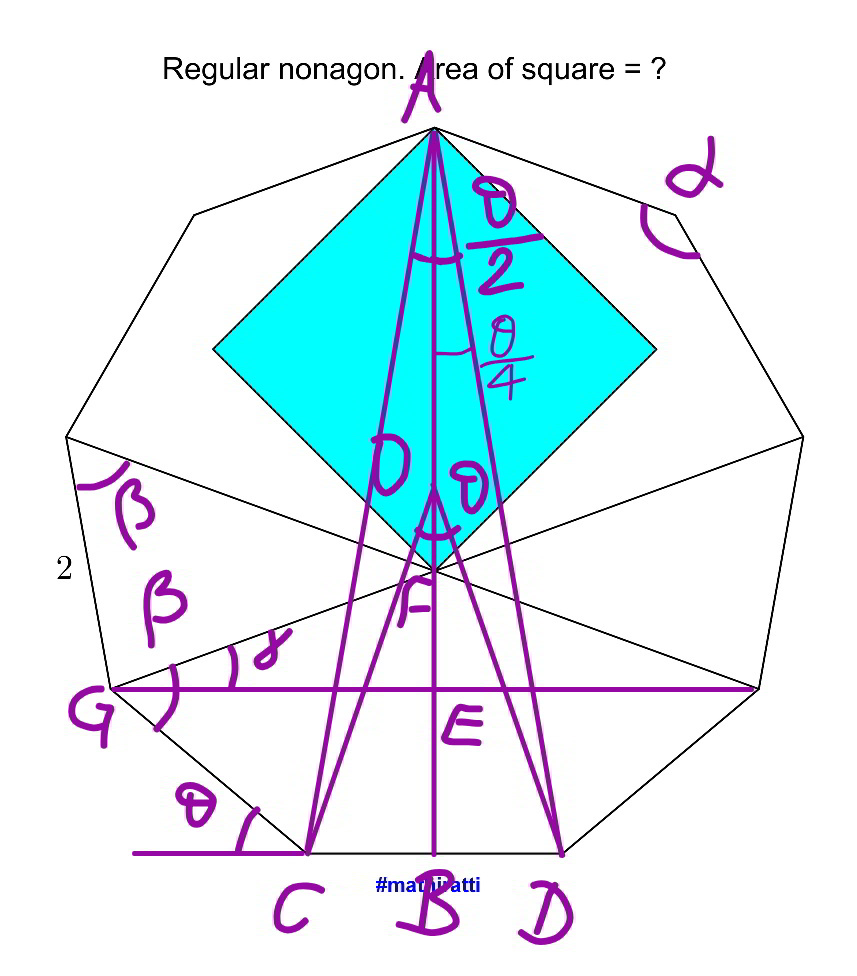
$$\alpha=\frac{\left({n}−\mathrm{2}\right)×\mathrm{180}°}{{n}}=\frac{\left(\mathrm{9}−\mathrm{2}\right)×\mathrm{180}}{\mathrm{9}}=\mathrm{140}° \\ $$$$\theta=\frac{\mathrm{360}°}{{n}}=\frac{\mathrm{360}}{\mathrm{9}}=\mathrm{40}° \\ $$$$\mathrm{2}\beta+\mathrm{3}\alpha=\mathrm{3}×\mathrm{180}° \\ $$$$\Rightarrow\beta=\frac{\mathrm{540}−\mathrm{420}}{\mathrm{2}}=\mathrm{60}° \\ $$$$\gamma=\beta−\theta=\mathrm{60}−\mathrm{40}=\mathrm{20}° \\ $$$${AB}=\frac{{BD}}{\mathrm{tan}\:\frac{\theta}{\mathrm{4}}}=\frac{{a}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{10}°} \\ $$$${EB}={CG}×\mathrm{sin}\:\theta={a}\:\mathrm{sin}\:\mathrm{40}° \\ $$$${GE}=\frac{{a}}{\mathrm{2}}+{a}\:\mathrm{cos}\:\theta=\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{40}°\right) \\ $$$${FE}={GE}×\mathrm{tan}\:\gamma=\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{40}°\right)\mathrm{tan}\:\mathrm{20}° \\ $$$${AF}={AB}−{FE}−{EB} \\ $$$${AF}=\frac{{a}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{10}°}−\frac{{a}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{40}°\right)\mathrm{tan}\:\mathrm{20}°−{a}\:\mathrm{sin}\:\mathrm{40}° \\ $$$$\frac{{AF}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{10}°}−\frac{\mathrm{tan}\:\mathrm{20}°}{\mathrm{2}}−\mathrm{cos}\:\mathrm{40}°\:\mathrm{tan}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{40}° \\ $$$$\frac{{AF}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{10}°}−\frac{\mathrm{tan}\:\mathrm{20}°}{\mathrm{2}}−\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{20}°−\mathrm{1}\right)\:\mathrm{tan}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{40}° \\ $$$$\frac{{AF}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{tan}\:\mathrm{10}°}+\frac{\mathrm{tan}\:\mathrm{20}°}{\mathrm{2}}−\mathrm{2}\:\mathrm{sin}\:\mathrm{40}° \\ $$$$\frac{{AF}}{{a}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{AF}=\sqrt{\mathrm{3}}{a} \\ $$$${area}\:{of}\:{square}\:=\left(\frac{{AF}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\frac{{AF}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{3}×\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{6} \\ $$
Commented by Tawa11 last updated on 29/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
