Menu Close

Question-77103

Tinku Tara 0 Comments
Pin




Question Number 77103 by Boyka last updated on 03/Jan/20
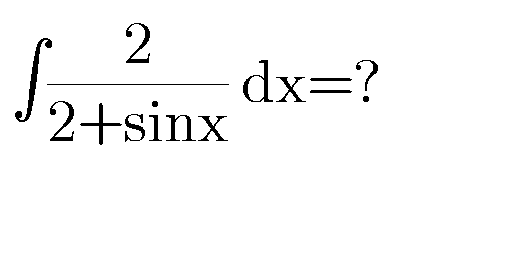
Commented by turbo msup by abdo last updated on 03/Jan/20
let I=∫ (2/(2+sinx))dx changement tan((x/2)) =t give I=∫ (2/(2+((2t)/(1+t^2 ))))×((2dt)/(1+t^2 )) =2 ∫ (dt/(1+t^2 +t)) =2 ∫ (dt/(t^2 +t+1)) =2∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) 2 ∫ (1/((3/4)(1+u^2 )))×((√3)/2)du =2×(4/3)×((√3)/2) arctanu +c =(4/( (√3))) arctan(((2t+1)/( (√3))))+c =(4/( (√3)))arctan(((2tan((x/2))+1)/( (√3)))) +C
$${let}\:{I}=\int\:\:\frac{\mathrm{2}}{\mathrm{2}+{sinx}}{dx}\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)\:={t}\:{give}\: \\ $$$${I}=\int\:\:\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+{t}} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:=\mathrm{2}\int\:\:\frac{{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{t}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\mathrm{2}\:\int\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$=\mathrm{2}×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{arctanu}\:+{c} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{c} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+{C} \\ $$
Answered by john santu last updated on 03/Jan/20
let tan ((x/2))=u. ⇒sin (x)= ((2u)/(1+u^2 )) dx = (2/(1+u^2 )) du . ⇒ 2+sin (x) = ((2u^2 +2u+2)/(1+u^2 )) ∫ (4/(2(u^2 +u+1))) du= ∫ ((2du)/((u+(1/2))^2 +(3/(4 )))) = 2×((√3)/2) tan^(−1) (tan ((x/2))+((√3)/2))+c = (√(3 ))tan^(−1) (tan ((x/2))+((√3)/2))+c ★
$${let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)={u}.\:\Rightarrow\mathrm{sin}\:\left({x}\right)=\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${dx}\:=\:\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du}\:.\:\Rightarrow\:\mathrm{2}+\mathrm{sin}\:\left({x}\right)\:=\:\frac{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\int\:\frac{\mathrm{4}}{\mathrm{2}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}\:{du}= \\ $$$$\int\:\:\frac{\mathrm{2}{du}}{\left({u}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}\:}}\:=\:\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{c} \\ $$$$=\:\sqrt{\mathrm{3}\:}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{c}\:\bigstar \\ $$
Commented by MJS last updated on 03/Jan/20
error line 2 must be 2+sin x =((2(t^2 +t+1))/(t^2 +1))
$$\mathrm{error} \\ $$$$\mathrm{line}\:\mathrm{2}\:\mathrm{must}\:\mathrm{be}\:\mathrm{2}+\mathrm{sin}\:{x}\:=\frac{\mathrm{2}\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by john santu last updated on 03/Jan/20
oh yes sir
$${oh}\:{yes}\:{sir} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *