Menu Close

Question-77234

Tinku Tara 0 Comments
Pin




Question Number 77234 by TawaTawa last updated on 04/Jan/20
Answered by mr W last updated on 04/Jan/20
=∫_0 ^1 x^(1/2) x^((1/2)×(1/3)) x^((1/2)×(1/3)×(1/4)) x^((1/2)×(1/3)×(1/4)×(1/5)) ...dx =∫_0 ^1 x^((1/(1×2))+(1/(1×2×3))+(1/(1×2×3×4))+(1/(1×2×3×4×5))+...) dx =∫_0 ^1 x^(Σ_(n=0) ^∞ (1/(n!))−2) dx =∫_0 ^1 x^(e−2) dx =(1/(e−1))[x^(e−1) ]_0 ^1 =(1/(e−1))
$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}} {x}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{5}}} …{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}×\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}}+…} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{e}−\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{{e}−\mathrm{1}}\left[{x}^{{e}−\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{e}−\mathrm{1}} \\ $$
Commented by TawaTawa last updated on 04/Jan/20
God bless you sir. I appreciate.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by TawaTawa last updated on 04/Jan/20
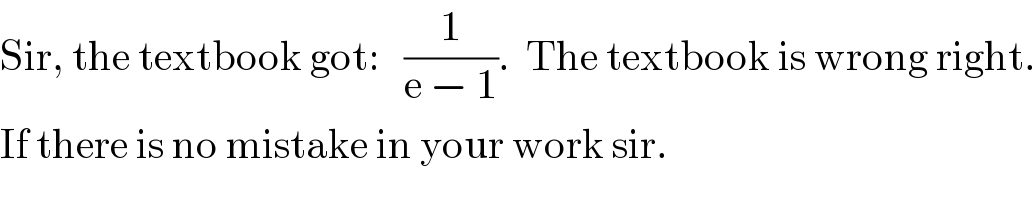
Sir, the textbook got: (1/(e − 1)). The textbook is wrong right. If there is no mistake in your work sir.
$$\mathrm{Sir},\:\mathrm{the}\:\mathrm{textbook}\:\mathrm{got}:\:\:\:\frac{\mathrm{1}}{\mathrm{e}\:−\:\mathrm{1}}.\:\:\mathrm{The}\:\mathrm{textbook}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{right}. \\ $$$$\mathrm{If}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{mistake}\:\mathrm{in}\:\mathrm{your}\:\mathrm{work}\:\mathrm{sir}.\: \\ $$
Commented by TawaTawa last updated on 04/Jan/20
And sir, how is the summation x^(e − 1)
$$\mathrm{And}\:\mathrm{sir},\:\mathrm{how}\:\mathrm{is}\:\mathrm{the}\:\mathrm{summation}\:\:\:\mathrm{x}^{\mathrm{e}\:−\:\mathrm{1}} \\ $$
Commented by TawaTawa last updated on 04/Jan/20
Thanks for your time sir
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 04/Jan/20
Commented by TawaTawa last updated on 04/Jan/20
Similar question sir.
$$\mathrm{Similar}\:\mathrm{question}\:\mathrm{sir}. \\ $$
Commented by Smail last updated on 04/Jan/20
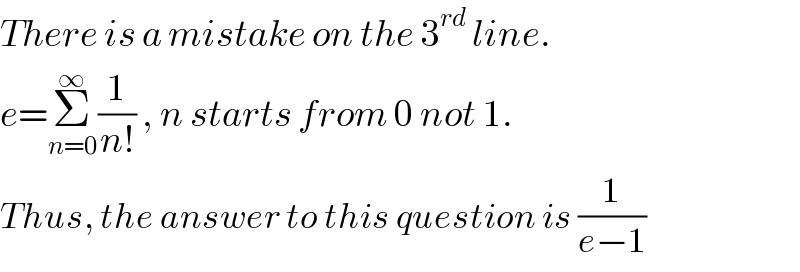
There is a mistake on the 3^(rd) line. e=Σ_(n=0) ^∞ (1/(n!)) , n starts from 0 not 1. Thus, the answer to this question is (1/(e−1))
$${There}\:{is}\:{a}\:{mistake}\:{on}\:{the}\:\mathrm{3}^{{rd}} \:{line}. \\ $$$${e}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\:,\:{n}\:{starts}\:{from}\:\mathrm{0}\:{not}\:\mathrm{1}. \\ $$$${Thus},\:{the}\:{answer}\:{to}\:{this}\:{question}\:{is}\:\frac{\mathrm{1}}{{e}−\mathrm{1}} \\ $$
Commented by TawaTawa last updated on 04/Jan/20
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 04/Jan/20
Thanks for correcting it sir Mrw.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{correcting}\:\mathrm{it}\:\mathrm{sir}\:\:\mathrm{Mrw}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *