Question-77252

Question Number 77252 by Maclaurin Stickker last updated on 04/Jan/20

Commented by Maclaurin Stickker last updated on 04/Jan/20

$${I}\:{don}'{t}\:{want}\:{the}\:{answer},\:{I}\:{want}\:{a}\:{tip} \\ $$$${on}\:{how}\:{to}\:{solve}.\: \\ $$

Commented by Maclaurin Stickker last updated on 04/Jan/20

$${I}\:{tried}\:{to}\:{find}\:{the}\:{radius}\:{of}\:{the} \\ $$$${largest}\:{circumference}\:{as}\:{a}\:{function} \\ $$$${of}\:{the}\:{radius}\:{of}\:{the}\:{yellow} \\ $$$${circumference}\:{but}\:{the}\:{results}\:{weren}'{t} \\ $$$${good}… \\ $$

Answered by mr W last updated on 05/Jan/20

Commented by Maclaurin Stickker last updated on 05/Jan/20

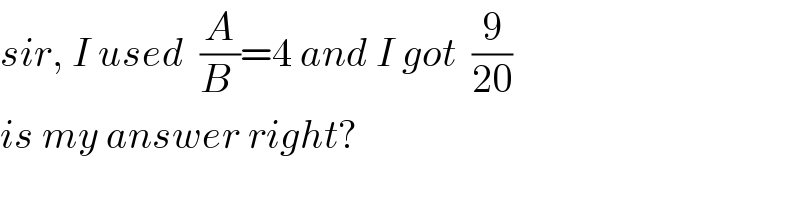
sir, I used (A/(B ))=4 and I got (9/(20)) is my answer right?

$${sir},\:{I}\:{used}\:\:\frac{{A}}{{B}\:}=\mathrm{4}\:{and}\:{I}\:{got}\:\:\frac{\mathrm{9}}{\mathrm{20}}\:\: \\ $$$${is}\:{my}\:{answer}\:{right}? \\ $$$$ \\ $$

Commented by mr W last updated on 05/Jan/20

O as origin and OF as x−axis x_A =−R+r_a x_C =2r_a −R x_B ^2 +y_B ^2 =(R−r_b )^2 (x_B +R−r_a )^2 +y_B ^2 =(r_a +r_b )^2 (x_B +R−r_a )^2 −x_B ^2 =(r_a +r_b )^2 −(R−r_b )^2 ⇒(2x_B +R−r_a )(R−r_a )=(R+r_a )(r_a +2r_b −R) ⇒x_B =(((R+r_a )(2r_b −R+r_a )−(R−r_a )^2 )/(2(R−r_a ))) ⇒y_B =(√((R−r_b )^2 −x_B ^2 )) CF=2(R−r_a ) ((EF)/(GF))=((2R)/(EF)) ⇒ EF^2 =2R(R−r_a ) EG^2 =EF^2 −GF^2 =2R(R−r_a )−(R−r_a )^2 EG^2 =(R−r_a )(R+r_a )=R^2 −r_a ^2 ⇒EG=(√(R^2 −r_a ^2 )) m=tan ∠ECG=((EG)/(CG))=((√(R^2 −r_a ^2 ))/(R−r_a ))=(√((R+r_a )/(R−r_a ))) x_C =2r_a −R eqn. of CE: y=m(x−x_C ) ⇒mx−y−m(2r_a −R)=0 r_b =((m(x_B +R−2r_a )−y_B )/( (√(1+m^2 )))) r_b =(((√((R−r_a )/(R+r_a )))(x_B +R−2r_a )−y_B )/( (√((2R)/(R+r_a ))))) ⇒r_b =(√((R−r_a )/(2R)))(x_B +R−2r_a )−(√((R+r_a )/(2R)))y_B let α=(r_a /R), β=(r_b /R) (x_B /R)=μ=(((1+α)(2β−1+α)−(1−α)^2 )/(2(1−α))) (y_B /R)=ν=(√((1−β)^2 −μ^2 )) ⇒β=(√((1−α)/2))(μ+1−2α)−(√((1+α)/2))ν ......

$${O}\:{as}\:{origin}\:{and}\:{OF}\:{as}\:{x}−{axis} \\ $$$${x}_{{A}} =−{R}+{r}_{{a}} \\ $$$${x}_{{C}} =\mathrm{2}{r}_{{a}} −{R} \\ $$$${x}_{{B}} ^{\mathrm{2}} +{y}_{{B}} ^{\mathrm{2}} =\left({R}−{r}_{{b}} \right)^{\mathrm{2}} \\ $$$$\left({x}_{{B}} +{R}−{r}_{{a}} \right)^{\mathrm{2}} +{y}_{{B}} ^{\mathrm{2}} =\left({r}_{{a}} +{r}_{{b}} \right)^{\mathrm{2}} \\ $$$$\left({x}_{{B}} +{R}−{r}_{{a}} \right)^{\mathrm{2}} −{x}_{{B}} ^{\mathrm{2}} =\left({r}_{{a}} +{r}_{{b}} \right)^{\mathrm{2}} −\left({R}−{r}_{{b}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{x}_{{B}} +{R}−{r}_{{a}} \right)\left({R}−{r}_{{a}} \right)=\left({R}+{r}_{{a}} \right)\left({r}_{{a}} +\mathrm{2}{r}_{{b}} −{R}\right) \\ $$$$\Rightarrow{x}_{{B}} =\frac{\left({R}+{r}_{{a}} \right)\left(\mathrm{2}{r}_{{b}} −{R}+{r}_{{a}} \right)−\left({R}−{r}_{{a}} \right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{r}_{{a}} \right)} \\ $$$$\Rightarrow{y}_{{B}} =\sqrt{\left({R}−{r}_{{b}} \right)^{\mathrm{2}} −{x}_{{B}} ^{\mathrm{2}} } \\ $$$$ \\ $$$${CF}=\mathrm{2}\left({R}−{r}_{{a}} \right) \\ $$$$\frac{{EF}}{{GF}}=\frac{\mathrm{2}{R}}{{EF}}\:\Rightarrow\:{EF}^{\mathrm{2}} =\mathrm{2}{R}\left({R}−{r}_{{a}} \right) \\ $$$${EG}^{\mathrm{2}} ={EF}^{\mathrm{2}} −{GF}^{\mathrm{2}} =\mathrm{2}{R}\left({R}−{r}_{{a}} \right)−\left({R}−{r}_{{a}} \right)^{\mathrm{2}} \\ $$$${EG}^{\mathrm{2}} =\left({R}−{r}_{{a}} \right)\left({R}+{r}_{{a}} \right)={R}^{\mathrm{2}} −{r}_{{a}} ^{\mathrm{2}} \\ $$$$\Rightarrow{EG}=\sqrt{{R}^{\mathrm{2}} −{r}_{{a}} ^{\mathrm{2}} } \\ $$$${m}=\mathrm{tan}\:\angle{ECG}=\frac{{EG}}{{CG}}=\frac{\sqrt{{R}^{\mathrm{2}} −{r}_{{a}} ^{\mathrm{2}} }}{{R}−{r}_{{a}} }=\sqrt{\frac{{R}+{r}_{{a}} }{{R}−{r}_{{a}} }} \\ $$$${x}_{{C}} =\mathrm{2}{r}_{{a}} −{R} \\ $$$${eqn}.\:{of}\:{CE}: \\ $$$${y}={m}\left({x}−{x}_{{C}} \right) \\ $$$$\Rightarrow{mx}−{y}−{m}\left(\mathrm{2}{r}_{{a}} −{R}\right)=\mathrm{0} \\ $$$${r}_{{b}} =\frac{{m}\left({x}_{{B}} +{R}−\mathrm{2}{r}_{{a}} \right)−{y}_{{B}} }{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$${r}_{{b}} =\frac{\sqrt{\frac{{R}−{r}_{{a}} }{{R}+{r}_{{a}} }}\left({x}_{{B}} +{R}−\mathrm{2}{r}_{{a}} \right)−{y}_{{B}} }{\:\sqrt{\frac{\mathrm{2}{R}}{{R}+{r}_{{a}} }}} \\ $$$$\Rightarrow{r}_{{b}} =\sqrt{\frac{{R}−{r}_{{a}} }{\mathrm{2}{R}}}\left({x}_{{B}} +{R}−\mathrm{2}{r}_{{a}} \right)−\sqrt{\frac{{R}+{r}_{{a}} }{\mathrm{2}{R}}}{y}_{{B}} \\ $$$${let}\:\alpha=\frac{{r}_{{a}} }{{R}},\:\beta=\frac{{r}_{{b}} }{{R}} \\ $$$$\frac{{x}_{{B}} }{{R}}=\mu=\frac{\left(\mathrm{1}+\alpha\right)\left(\mathrm{2}\beta−\mathrm{1}+\alpha\right)−\left(\mathrm{1}−\alpha\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\alpha\right)} \\ $$$$\frac{{y}_{{B}} }{{R}}=\nu=\sqrt{\left(\mathrm{1}−\beta\right)^{\mathrm{2}} −\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\beta=\sqrt{\frac{\mathrm{1}−\alpha}{\mathrm{2}}}\left(\mu+\mathrm{1}−\mathrm{2}\alpha\right)−\sqrt{\frac{\mathrm{1}+\alpha}{\mathrm{2}}}\nu \\ $$$$…… \\ $$

Commented by mr W last updated on 05/Jan/20

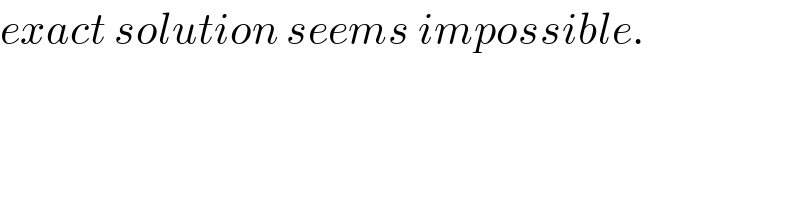
$${exact}\:{solution}\:{seems}\:{impossible}. \\ $$

Commented by Maclaurin Stickker last updated on 05/Jan/20

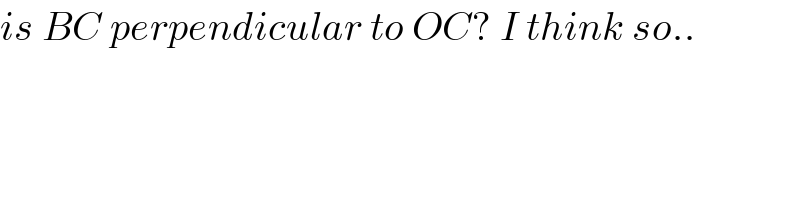
$${is}\:{BC}\:{perpendicular}\:{to}\:{OC}?\:{I}\:{think}\:{so}.. \\ $$

Commented by Maclaurin Stickker last updated on 05/Jan/20

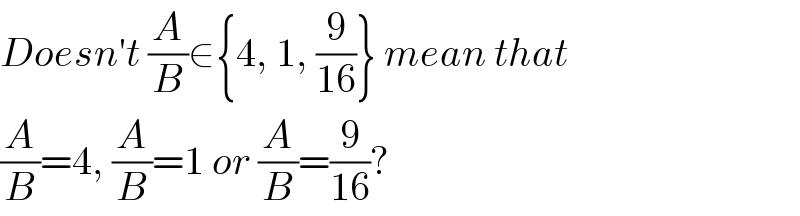
Doesn′t (A/B)∈{4, 1, (9/(16))} mean that (A/B)=4, (A/B)=1 or (A/B)=(9/(16))?

$${Doesn}'{t}\:\frac{{A}}{{B}}\in\left\{\mathrm{4},\:\mathrm{1},\:\frac{\mathrm{9}}{\mathrm{16}}\right\}\:{mean}\:{that} \\ $$$$\frac{{A}}{{B}}=\mathrm{4},\:\frac{{A}}{{B}}=\mathrm{1}\:{or}\:\frac{{A}}{{B}}=\frac{\mathrm{9}}{\mathrm{16}}? \\ $$

Commented by mr W last updated on 05/Jan/20