Question Number 77339 by naka3546 last updated on 05/Jan/20
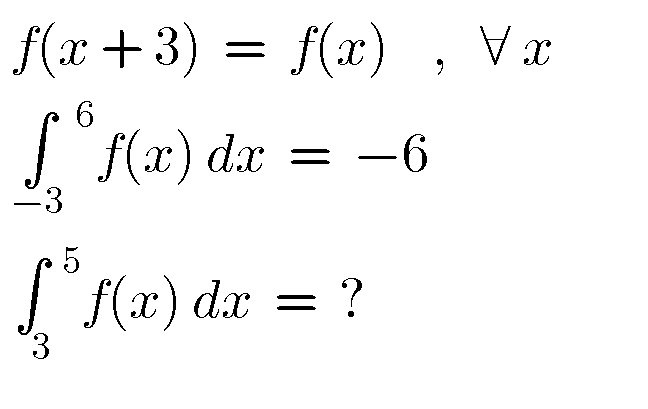
Commented by mr W last updated on 05/Jan/20
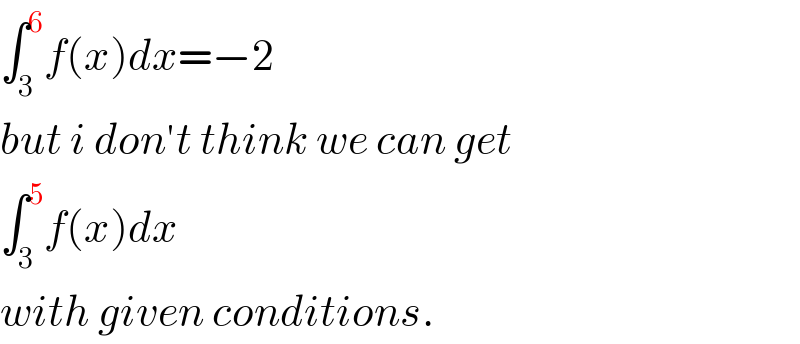
$$\int_{\mathrm{3}} ^{\mathrm{6}} {f}\left({x}\right){dx}=−\mathrm{2} \\ $$$${but}\:{i}\:{don}'{t}\:{think}\:{we}\:{can}\:{get} \\ $$$$\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx} \\ $$$${with}\:{given}\:{conditions}. \\ $$
Commented by msup trace by abdo last updated on 05/Jan/20
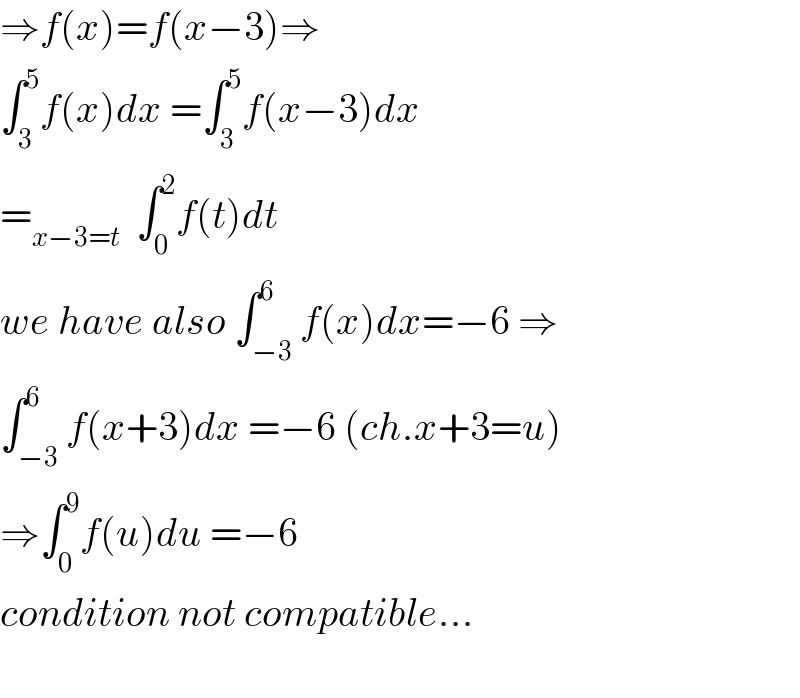
$$\Rightarrow{f}\left({x}\right)={f}\left({x}−\mathrm{3}\right)\Rightarrow \\ $$$$\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}\right){dx}\:=\int_{\mathrm{3}} ^{\mathrm{5}} {f}\left({x}−\mathrm{3}\right){dx} \\ $$$$=_{{x}−\mathrm{3}={t}} \:\:\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({t}\right){dt} \\ $$$${we}\:{have}\:{also}\:\int_{−\mathrm{3}} ^{\mathrm{6}} {f}\left({x}\right){dx}=−\mathrm{6}\:\Rightarrow \\ $$$$\int_{−\mathrm{3}} ^{\mathrm{6}} {f}\left({x}+\mathrm{3}\right){dx}\:=−\mathrm{6}\:\left({ch}.{x}+\mathrm{3}={u}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{9}} {f}\left({u}\right){du}\:=−\mathrm{6} \\ $$$${condition}\:{not}\:{compatible}… \\ $$$$ \\ $$
Answered by john santu last updated on 06/Jan/20
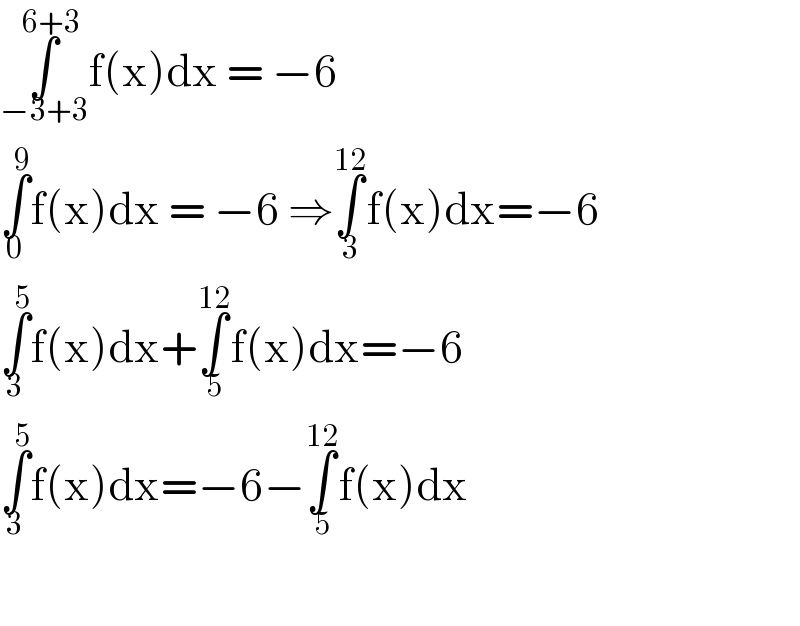
$$\underset{−\mathrm{3}+\mathrm{3}} {\overset{\mathrm{6}+\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:−\mathrm{6} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{9}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:−\mathrm{6}\:\Rightarrow\underset{\mathrm{3}} {\overset{\mathrm{12}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=−\mathrm{6} \\ $$$$\underset{\mathrm{3}} {\overset{\mathrm{5}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}+\underset{\mathrm{5}} {\overset{\mathrm{12}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=−\mathrm{6} \\ $$$$\underset{\mathrm{3}} {\overset{\mathrm{5}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=−\mathrm{6}−\underset{\mathrm{5}} {\overset{\mathrm{12}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$ \\ $$
