Question Number 7738 by 314159 last updated on 13/Sep/16
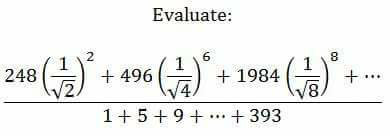
Commented by Rasheed Soomro last updated on 13/Sep/16
![((248((1/( (√2))))^2 +496((1/( (√4))))^6 +1984((1/( (√8))))^8 +...)/(1+5+9+...393)) ((248((1/2))^1 +496((1/4))^3 +1984((1/8))^4 +...)/(1+5+9+...393)) −−−−−−−−−−−−−−−− 1+5+9+....+393 a=1st term=1 , d=common difference=5−1=4 T_n =nth term=393 T_n =a+(n−1)d=1+(n−1)(4)=393 =4n−3=393 n=((396)/4)=99 S=1+5+9+...+393 S=(n/2)[a+l] , l=last term =((99)/2)[1+393]=197×99 −−−−−−−−−−−−−−− ((124((1/2))^0 +124((1/4))^2 +248((1/8))^3 +...)/(197×99)) Continue](https://www.tinkutara.com/question/Q7740.png)
$$\frac{\mathrm{248}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{496}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}\right)^{\mathrm{6}} +\mathrm{1984}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}}}\right)^{\mathrm{8}} +…}{\mathrm{1}+\mathrm{5}+\mathrm{9}+…\mathrm{393}} \\ $$$$\frac{\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{1}} +\mathrm{496}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} +\mathrm{1984}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{4}} +…}{\mathrm{1}+\mathrm{5}+\mathrm{9}+…\mathrm{393}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$$\mathrm{1}+\mathrm{5}+\mathrm{9}+….+\mathrm{393} \\ $$$${a}=\mathrm{1}{st}\:{term}=\mathrm{1}\:,\:{d}={common}\:{difference}=\mathrm{5}−\mathrm{1}=\mathrm{4} \\ $$$${T}_{{n}} ={nth}\:{term}=\mathrm{393} \\ $$$${T}_{{n}} ={a}+\left({n}−\mathrm{1}\right){d}=\mathrm{1}+\left({n}−\mathrm{1}\right)\left(\mathrm{4}\right)=\mathrm{393} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{n}−\mathrm{3}=\mathrm{393} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}=\frac{\mathrm{396}}{\mathrm{4}}=\mathrm{99} \\ $$$${S}=\mathrm{1}+\mathrm{5}+\mathrm{9}+…+\mathrm{393} \\ $$$${S}=\frac{{n}}{\mathrm{2}}\left[{a}+{l}\right]\:\:\:\:\:,\:{l}={last}\:{term} \\ $$$$\:\:\:\:=\frac{\mathrm{99}}{\mathrm{2}}\left[\mathrm{1}+\mathrm{393}\right]=\mathrm{197}×\mathrm{99} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\frac{\mathrm{124}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{0}} +\mathrm{124}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{3}} +…}{\mathrm{197}×\mathrm{99}} \\ $$$${Continue} \\ $$$$ \\ $$
Commented by prakash jain last updated on 13/Sep/16
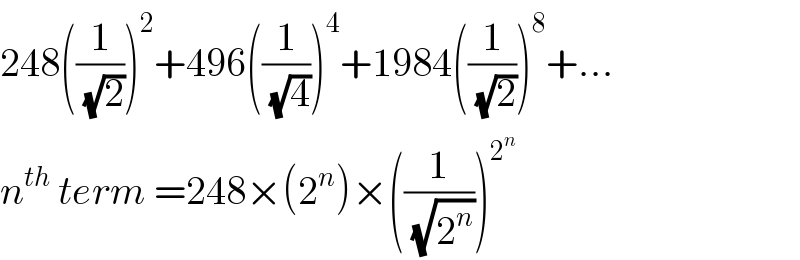
$$\mathrm{248}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{496}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}\right)^{\mathrm{4}} +\mathrm{1984}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{8}} +… \\ $$$${n}^{{th}} \:{term}\:=\mathrm{248}×\left(\mathrm{2}^{{n}} \right)×\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}^{{n}} }}\right)^{\mathrm{2}^{{n}} } \\ $$
Commented by Rasheed Soomro last updated on 13/Sep/16

$${That}\:{means}\:{there}'{s}\:{a}\:{mistake}\:{in}\:{the}\:{statement} \\ $$$${of}\:{the}\:{question}!\:{That}\:{was}\:{also}\:{my}\:{guess}. \\ $$
Commented by sandy_suhendra last updated on 13/Sep/16
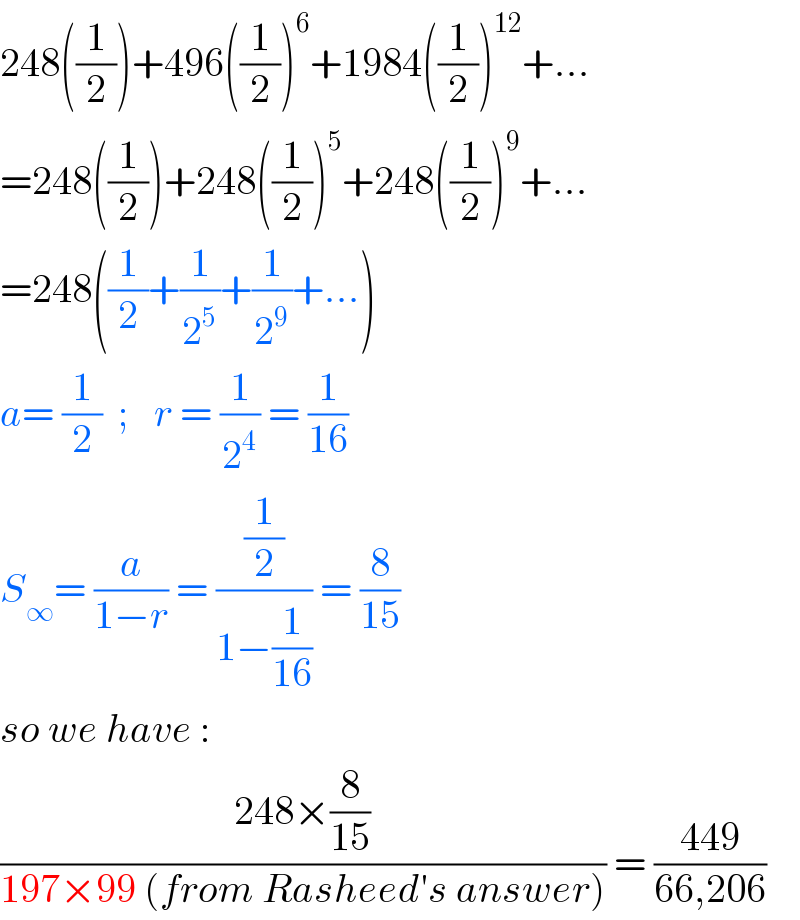
$$\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{496}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{6}} +\mathrm{1984}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{12}} +… \\ $$$$=\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{5}} +\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{9}} +… \\ $$$$=\mathrm{248}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{9}} }+…\right) \\ $$$${a}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:;_{} \:\:{r}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${S}_{\infty} =\:\frac{{a}}{\mathrm{1}−{r}}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}}\:=\:\frac{\mathrm{8}}{\mathrm{15}} \\ $$$${so}\:{we}\:{have}\:: \\ $$$$\frac{\mathrm{248}×\frac{\mathrm{8}}{\mathrm{15}}}{\mathrm{197}×\mathrm{99}\:\left({from}\:{Rasheed}'{s}\:{answer}\right)}\:=\:\frac{\mathrm{449}}{\mathrm{66},\mathrm{206}} \\ $$
Commented by Rasheed Soomro last updated on 14/Sep/16

$$\mathcal{N}{ice}!\:\: \\ $$
Commented by prakash jain last updated on 13/Sep/16
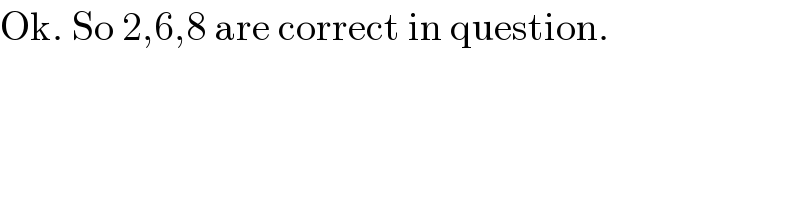
$$\mathrm{Ok}.\:\mathrm{So}\:\mathrm{2},\mathrm{6},\mathrm{8}\:\mathrm{are}\:\mathrm{correct}\:\mathrm{in}\:\mathrm{question}. \\ $$
