Question-77412

Question Number 77412 by BK last updated on 06/Jan/20

Commented by Tony Lin last updated on 06/Jan/20

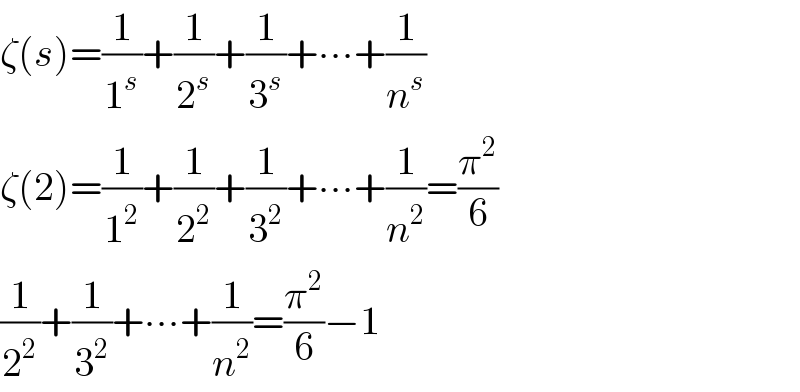
ζ(s)=(1/1^s )+(1/2^s )+(1/3^s )+∙∙∙+(1/n^s ) ζ(2)=(1/1^2 )+(1/2^2 )+(1/3^2 )+∙∙∙+(1/n^2 )=(π^2 /6) (1/2^2 )+(1/3^2 )+∙∙∙+(1/n^2 )=(π^2 /6)−1

$$\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{{s}} } \\ $$$$\zeta\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$

Commented by mr W last updated on 06/Jan/20

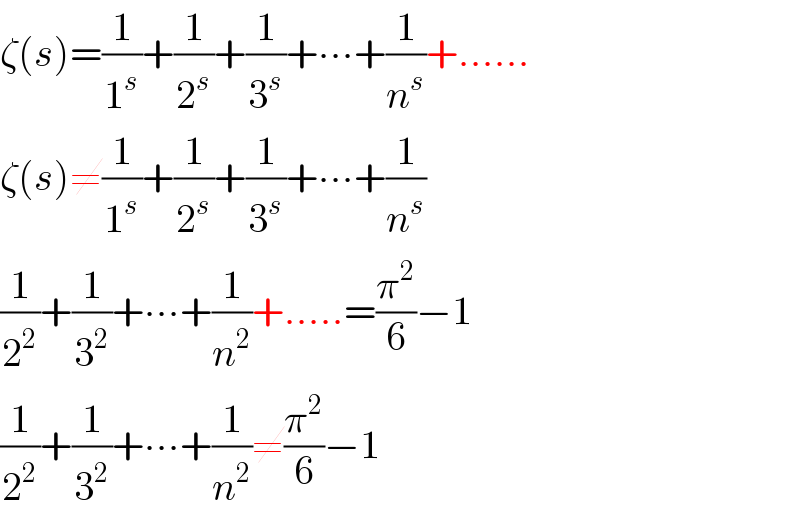
ζ(s)=(1/1^s )+(1/2^s )+(1/3^s )+∙∙∙+(1/n^s )+...... ζ(s)≠(1/1^s )+(1/2^s )+(1/3^s )+∙∙∙+(1/n^s ) (1/2^2 )+(1/3^2 )+∙∙∙+(1/n^2 )+.....=(π^2 /6)−1 (1/2^2 )+(1/3^2 )+∙∙∙+(1/n^2 )≠(π^2 /6)−1

$$\zeta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{{s}} }+…… \\ $$$$\zeta\left({s}\right)\neq\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{{s}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+…..=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\neq\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$

Commented by BK last updated on 06/Jan/20

$$\mathrm{thanks} \\ $$

Commented by Tony Lin last updated on 06/Jan/20

$${sorry}\:{I}\:{got}\:{it} \\ $$

Commented by BK last updated on 06/Jan/20

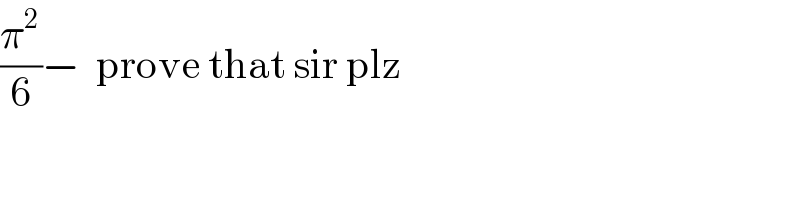
$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\:\:\mathrm{prove}\:\mathrm{that}\:\mathrm{sir}\:\mathrm{plz} \\ $$

Commented by mathmax by abdo last updated on 06/Jan/20

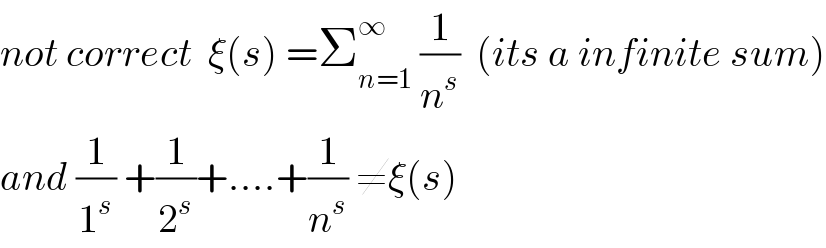
not correct ξ(s) =Σ_(n=1) ^∞ (1/n^s ) (its a infinite sum) and (1/1^s ) +(1/2^s )+....+(1/n^s ) ≠ξ(s)

$${not}\:{correct}\:\:\xi\left({s}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{{s}} }\:\:\left({its}\:{a}\:{infinite}\:{sum}\right) \\ $$$${and}\:\frac{\mathrm{1}}{\mathrm{1}^{{s}} }\:+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+….+\frac{\mathrm{1}}{{n}^{{s}} }\:\neq\xi\left({s}\right) \\ $$

Commented by mathmax by abdo last updated on 07/Jan/20

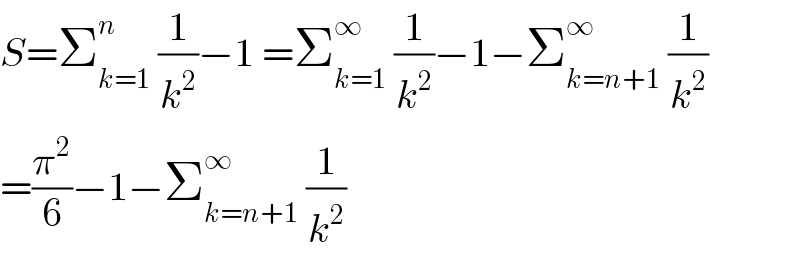
S=Σ_(k=1) ^n (1/k^2 )−1 =Σ_(k=1) ^∞ (1/k^2 )−1−Σ_(k=n+1) ^∞ (1/k^2 ) =(π^2 /6)−1−Σ_(k=n+1) ^∞ (1/k^2 )

$${S}=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}−\sum_{{k}={n}+\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}−\sum_{{k}={n}+\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply