Question Number 77425 by mr W last updated on 06/Jan/20

Commented by mr W last updated on 06/Jan/20

$${Given}:\:{r}_{{a}} ,\:{r}_{{b}} ,\:{r}_{{c}} \\ $$$${Find}:\:{r}=? \\ $$$$ \\ $$$$\left({see}\:{also}\:{Q}\mathrm{77229}\right) \\ $$
Commented by jagoll last updated on 06/Jan/20
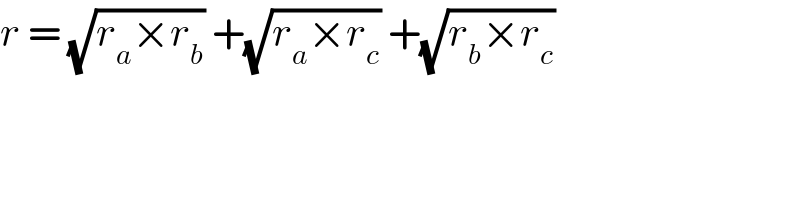
$${r}\:=\:\sqrt{{r}_{{a}} ×{r}_{{b}} }\:+\sqrt{{r}_{{a}} ×{r}_{{c}} }\:+\sqrt{{r}_{{b}} ×{r}_{{c}} } \\ $$
Answered by mr W last updated on 06/Jan/20

Commented by mr W last updated on 06/Jan/20

$${Found}\:{an}\:{other}\:{way}\:{than}\:{in}\:{Q}\mathrm{77229}: \\ $$$$\mathrm{cos}\:\alpha=\frac{{r}−{r}_{{a}} }{{r}+{r}_{{a}} }\:\:\Rightarrow\:\mathrm{sin}\:\alpha=\frac{\mathrm{2}\sqrt{{rr}_{{a}} }}{{r}+{r}_{{a}} } \\ $$$$\mathrm{cos}\:\beta=\frac{{r}−{r}_{{b}} }{{r}+{r}_{{b}} }\:\:\Rightarrow\:\mathrm{sin}\:\beta=\frac{\mathrm{2}\sqrt{{rr}_{{b}} }}{{r}+{r}_{{b}} } \\ $$$$\mathrm{cos}\:\gamma=\frac{{r}−{r}_{{c}} }{{r}+{r}_{{c}} } \\ $$$$\mathrm{2}\alpha+\mathrm{2}\beta+\mathrm{2}\gamma=\mathrm{2}\pi \\ $$$$\Rightarrow\alpha+\beta+\gamma=\pi \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\left(\pi−\gamma\right)=−\mathrm{cos}\:\gamma \\ $$$$\frac{{r}−{r}_{{a}} }{{r}+{r}_{{a}} }×\frac{{r}−{r}_{{b}} }{{r}+{r}_{{b}} }−\frac{\mathrm{2}\sqrt{{rr}_{{a}} }}{{r}+{r}_{{a}} }×\frac{\mathrm{2}\sqrt{{rr}_{{b}} }}{{r}+{r}_{{b}} }=−\frac{{r}−{r}_{{c}} }{{r}+{r}_{{c}} } \\ $$$$\frac{\left({r}−{r}_{{a}} \right)\left({r}−{r}_{{b}} \right)−\mathrm{4}{r}\sqrt{{r}_{{a}} {r}_{{b}} }}{\left({r}+{r}_{{a}} \right)\left({r}+{r}_{{b}} \right)}=−\frac{{r}−{r}_{{c}} }{{r}+{r}_{{c}} } \\ $$$$\frac{{r}^{\mathrm{2}} −\left({r}_{{a}} +{r}_{{b}} +\mathrm{4}\sqrt{{r}_{{a}} {r}_{{b}} }\right){r}+{r}_{{a}} {r}_{{b}} }{{r}^{\mathrm{2}} +\left({r}_{{a}} +{r}_{{b}} \right){r}+{r}_{{a}} {r}_{{b}} }=−\frac{{r}−{r}_{{c}} }{{r}+{r}_{{c}} } \\ $$$${r}^{\mathrm{3}} −\left({r}_{{a}} +{r}_{{b}} +\mathrm{4}\sqrt{{r}_{{a}} {r}_{{b}} }\right){r}^{\mathrm{2}} +{r}_{{a}} {r}_{{b}} {r}+{r}_{{c}} {r}^{\mathrm{2}} −\left({r}_{{c}} {r}_{{a}} +{r}_{{b}} {r}_{{c}} +\mathrm{4}{r}_{{c}} \sqrt{{r}_{{a}} {r}_{{b}} }\right){r}+{r}_{{a}} {r}_{{b}} {r}_{{c}} \\ $$$$\:\:\:\:+{r}^{\mathrm{3}} +\left({r}_{{a}} +{r}_{{b}} \right){r}^{\mathrm{2}} +{r}_{{a}} {r}_{{b}} {r}−{r}_{{c}} {r}^{\mathrm{2}} −\left({r}_{{c}} {r}_{{a}} +{r}_{{b}} {r}_{{c}} \right){r}−{r}_{{a}} {r}_{{b}} {r}_{{c}} =\mathrm{0} \\ $$$${r}^{\mathrm{3}} −\mathrm{2}\sqrt{{r}_{{a}} {r}_{{b}} }{r}^{\mathrm{2}} +{r}_{{a}} {r}_{{b}} {r}−{r}_{{c}} \left({r}_{{a}} +{r}_{{b}} +\mathrm{2}\sqrt{{r}_{{a}} {r}_{{b}} }\right){r}=\mathrm{0} \\ $$$${r}^{\mathrm{2}} −\mathrm{2}\sqrt{{r}_{{a}} {r}_{{b}} }{r}+{r}_{{a}} {r}_{{b}} −{r}_{{c}} \left(\sqrt{{r}_{{a}} }+\sqrt{{r}_{{b}} }\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({r}−\sqrt{{r}_{{a}} {r}_{{b}} }\right)^{\mathrm{2}} −\left(\sqrt{{r}_{{c}} {r}_{{a}} }+\sqrt{{r}_{{b}} {r}_{{c}} }\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${r}−\sqrt{{r}_{{a}} {r}_{{b}} }=\pm\left(\sqrt{{r}_{{c}} {r}_{{a}} }+\sqrt{{r}_{{b}} {r}_{{c}} }\right) \\ $$$${r}=\sqrt{{r}_{{a}} {r}_{{b}} }\pm\left(\sqrt{{r}_{{c}} {r}_{{a}} }+\sqrt{{r}_{{b}} {r}_{{c}} }\right) \\ $$$${since}\:{r}>\mathrm{0},>{r}_{{a}} ,>{r}_{{b}} ,>{r}_{{c}} \\ $$$$\Rightarrow{r}=\sqrt{{r}_{{a}} {r}_{{b}} }+\sqrt{{r}_{{b}} {r}_{{c}} }+\sqrt{{r}_{{c}} {r}_{{a}} } \\ $$
Commented by behi83417@gmail.com last updated on 06/Jan/20

$$\mathrm{AmAzInG}\:\mathrm{proph}:\:\mathrm{mrW}! \\ $$$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 06/Jan/20
$${thank}\:{you}\:{sir}! \\ $$$${i}\:{remember}\:{that}\:{you}\:{once}\:{posted} \\ $$$${this}\:{question},\:{but}\:{i}\:{didn}'{t}\:{take} \\ $$$${much}\:{notice}. \\ $$
Commented by Maclaurin Stickker last updated on 06/Jan/20
$${Great}\:{method},\:{sir}.\:{Thanks}\:{for}\:{your}\:{work}. \\ $$
Commented by Tawa11 last updated on 29/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
